8350. Найдите геометрическое место центров шаров данного радиуса, касающихся граней данного двугранного угла.
Ответ. Прямая, параллельная ребру данного двугранного угла и удалённая от его граней на расстояние, равное данному радиусу.
Решение. Пусть O
— центр шара данного радиуса r
; A
и B
— точки касания шара с гранями \alpha
и \beta
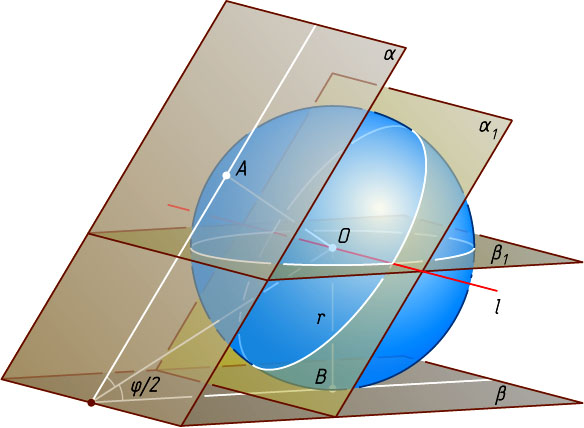
данного двугранного угла. Тогда OA\perp\alpha
, OA=r
. Это значит, что точка O
удалена от грани \alpha
на расстояние r
. Поэтому точка O
лежит в плоскости \alpha_{1}
, параллельной грани \alpha
и удалённой от неё на расстояние r
. Кроме того, точка O
лежит внутри данного двугранного угла. Значит, плоскость \alpha_{1}
единственна. Аналогично, точка O
лежит в одной из двух плоскостей \beta_{1}
, параллельных грани \beta
и удалённых от неё на расстояние r
. Следовательно, точка O
лежит на прямой l
пересечения плоскостей \alpha_{1}
и \beta_{1}
. Прямая l
параллельна ребру двугранного угла и удалена от него на расстояние \frac{r}{\cos\frac{\varphi}{2}}
, где \varphi
— величина данного двугранного угла.
Очевидно, что каждая точка прямой l
является центром шара радиуса r
, вписанного в данный двугранный угол.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5, с. 84
