8351. Шар радиуса R
касается плоскости \alpha
. Рассмотрим всевозможные шары радиуса r
, касающиеся данного шара и плоскости \alpha
. Найдите геометрические места центров этих шаров и точек их касания с плоскостью и данным шаром.
Ответ. Окружности радиусов 2\sqrt{Rr}
, 2\sqrt{Rr}
и \frac{2R\sqrt{Rr}}{R+r}
.
Указание. Линия центров двух касающихся шаров проходит через их точку касания.
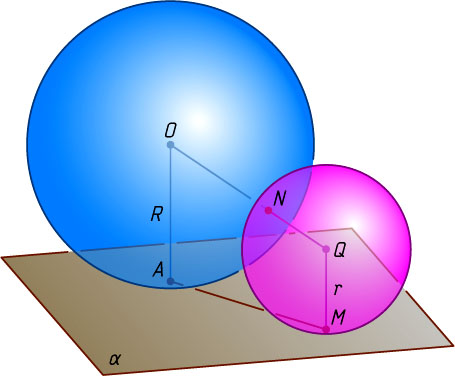
Решение. Пусть O
— центр данного шара радиуса R
, A
— точка касания этого шара с данной плоскостью \alpha
, Q
— центр произвольного шара радиуса r
, касающегося плоскости \alpha
в точке M
, а данного шара — в точке N
.
Так как OA\perp\alpha
и QM\perp\alpha
, то OA\parallel QM
. Через параллельные прямые OA
и QM
проведём плоскость. Точка N
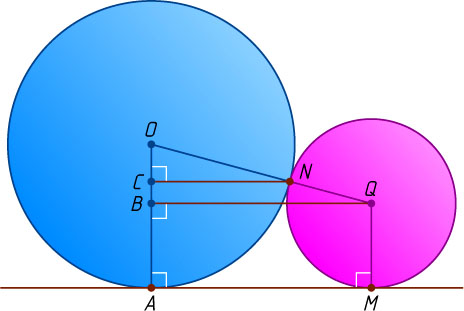
лежит в этой плоскости, так как линия центров двух касающихся шаров проходит через их точку касания. Опустим перпендикуляры QB
и NC
из точек Q
и N
на прямую OA
. Далее находим:
OB=OA-AB=OA-QM=R-r,
QB=\sqrt{OQ^{2}-OB^{2}}=\sqrt{(R+r)^{2}-(R-r)^{2}}=2\sqrt{Rr},
CN=BQ\cdot\frac{ON}{OQ}=2\sqrt{Rr}\cdot\frac{R}{R+r}=\frac{2R\sqrt{Rr}}{R+r},
OC=OB\cdot\frac{ON}{OQ}=(R-r)\cdot\frac{R}{R+r}=\frac{R(R-r)}{R+r},
AC=OA-OC=R-\frac{R(R-r)}{R+r}=\frac{2rR}{R+r}.
Отсюда вытекают следующие утверждения. Точка Q
лежит на окружности радиуса 2\sqrt{Rr}
с центром в фиксированной точке B
. Плоскость этой окружности проходит через точку B
параллельно плоскости \alpha
и удалена от плоскости \alpha
на расстояние r
. Очевидно, что каждая точка этой окружности является центром шара радиуса r
, касающегося плоскости \alpha
и данного шара радиуса R
.
Точка M
лежит на окружности радиуса 2\sqrt{Rr}
с центром в точке A
. Очевидно, что каждая точка этой окружности является точкой касания плоскости \alpha
с шаром радиуса r
, касающимся также данного шара радиуса R
.
Точка N
лежит на окружности радиуса \frac{2R\sqrt{Rr}}{R+r}
с центром в фиксированной точке C
. Плоскость этой окружности проходит через точку C
параллельно плоскости \alpha
и удалена от плоскости \alpha
на расстояние \frac{2rR}{R+r}
. Очевидно, что каждая точка этой окружности является точкой касания данного шара с некоторым шаром радиуса r
, касающимся также плоскости \alpha
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 6, с. 85

