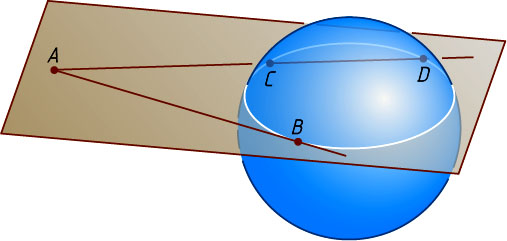
8352. Через точку A
, расположенную вне сферы, проведены две прямые. Одна из них касается сферы в точке B
, а вторая пересекает её в точках C
и D
. Докажите, что AB^{2}=AC\cdot AD
.
Указание. Примените теорему о касательной и секущей на плоскости.
Решение. Рассмотрим сечение сферы плоскостью, проходящей через пересекающиеся прямые AB
и AC
. Получим окружность, к которой из точки A
проведены касательная AB
(B
— точка касания) и секущая ACD
. По теореме о касательной и секущей AB^{2}=AC\cdot AD
. Что и требовалось доказать.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 7, с. 85
