8356. Стороны треугольника равны a
, b
и c
. Три шара попарно касаются друг друга и плоскости треугольника в его вершинах. Найдите радиусы шаров.
Ответ. \frac{bc}{2a}
, \frac{ac}{2b}
, \frac{ab}{2c}
.
Указание. См. задачу 365.
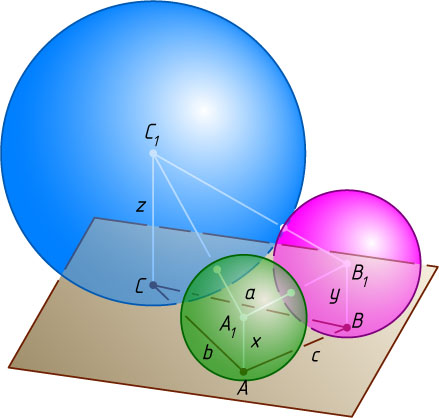
Решение. Пусть шары радиусов x
, y
и z
с центрами A_{1}
, B_{1}
и C_{1}
касаются плоскости треугольника ABC
со сторонами AB=c
, AC=b
и BC=a
в вершинах A
, B
и C
соответственно (рис. 1). Проведём плоскость через параллельные прямые CC_{1}
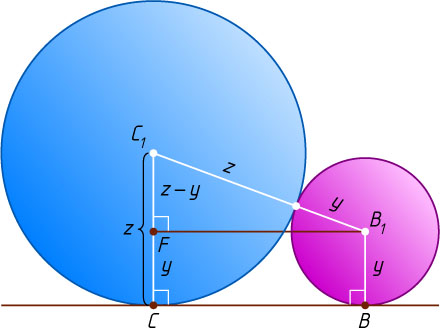
и BB_{1}
. Получим две касающиеся окружности радиусов y
и z
и прямую, касающуюся этих окружностей в точках B
и C
(рис. 2). Из точки B_{1}
опустим перпендикуляр B_{1}F
на прямую CC_{1}
. Тогда
C_{1}F=|CC_{1}-CF|=|CC_{1}-BB_{1}|=|z-y|,
a^{2}=BC^{2}=B_{1}F^{2}=B_{1}C_{1}^{2}-C_{1}F^{2}=(z+y)^{2}-(z-y)^{2}=4yz.
Аналогично, b^{2}=4xz
и c^{2}=4xy
. Таким образом, мы получили систему уравнений относительно x
, y
и z
:
\syst{yz=\frac{a^{2}}{4}\\xz=\frac{b^{2}}{4}\\xy=\frac{c^{2}}{4}.\\}
Перемножив почленно второе и третье уравнение и разделив результат на первое, получим, что x^{2}=\frac{b^{2}c^{2}}{4a^{2}}
. Следовательно, x=\frac{bc}{2a}
. Аналогично найдём y
и z
.
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 4.2, с. 62
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 4.2, с. 46
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 10, с. 85
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 2000 (устный экзамен)

