8358. Докажите, что в любую треугольную пирамиду можно вписать единственную сферу.
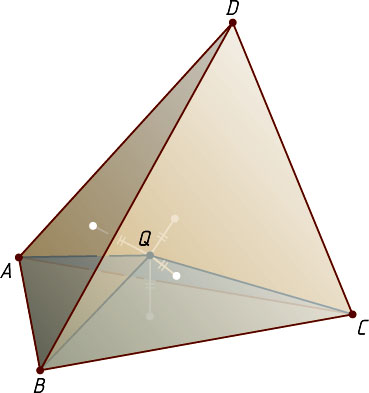
Решение. Рассмотрим треугольную пирамиду ABCD
. Биссекторные плоскости двугранных углов при рёбрах AB
, AC
и BD
имеют единственную общую точку Q
. Эта точка равноудалена от плоскостей всех четырёх граней пирамиды ABCD
. Следовательно, Q
— центр сферы, вписанной в пирамиду ABCD
.
Пусть O
— центр ещё одной сферы, вписанной в пирамиду ABCD
. Тогда точка O
равноудалена от всех граней пирамиды. Поэтому она совпадает с точкой Q
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — с. 87
