8362. Сторона основания правильной четырёхугольной пирамиды равна a
, боковое ребро равно b
. Найдите радиус описанного шара.
Ответ. \frac{b^{2}\sqrt{2}}{2\sqrt{2b^{2}-a^{2}}}
.
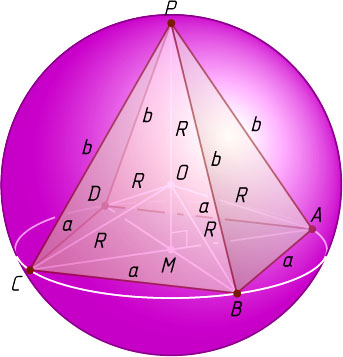
Решение. Первый способ. Пусть PM
— высота правильной четырёхугольной пирамиды PABCD
, R
— искомый радиус (рис. 1). Поскольку пирамида правильная, центр её описанной сферы лежит на прямой PM
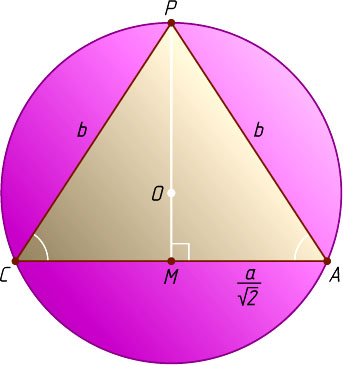
. Рассмотрим сечение пирамиды плоскостью, проходящей через прямую PM
и точку A
(рис. 2). Получим окружность радиуса R
с центром на прямой PM
, проходящую через точки P
, A
и C
. Тогда R
— радиус окружности, описанной около равнобедренного треугольника APC
, в котором
AP=CP=b,~AC=a\sqrt{2},~AM=\frac{a\sqrt{2}}{2}.
Из прямоугольного треугольника APM
находим, что
\cos\angle PAM=\frac{AM}{AP}=\frac{a\sqrt{2}}{2b}=\frac{a}{b\sqrt{2}}.
Поэтому
\sin\angle PAM=\sqrt{1-\cos^{2}\angle PAM}=\sqrt{1-\frac{a^{2}}{2b^{2}}}=\frac{\sqrt{2b^{2}-a^{2}}}{b\sqrt{2}}.
Следовательно,
R=\frac{CP}{2\sin\angle CAP}=\frac{CP}{2\sin\angle PAM}=\frac{b}{\frac{2\sqrt{2b^{2}-a^{2}}}{b\sqrt{2}}}=\frac{b^{2}\sqrt{2}}{2\sqrt{2b^{2}-a^{2}}}.
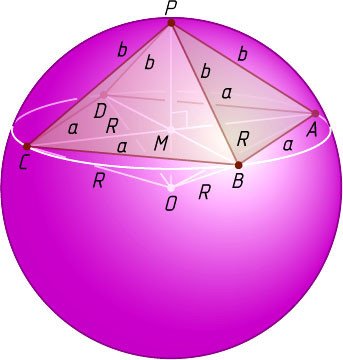
Второй способ. Пусть O
— центр сферы, описанной около правильной четырёхугольной пирамиды PABCD
с вершиной P
(рис. 1). Поскольку пирамида правильная, точка O
лежит на её высоте PM
. Из прямоугольных треугольников PAM
и OAM
находим, что
PM=\sqrt{AP^{2}-AM^{2}}=\sqrt{b^{2}-\left(\frac{a}{\sqrt{2}}\right)^{2}}=\frac{\sqrt{2b^{2}-a^{2}}}{\sqrt{2}},
OM=\sqrt{OA^{2}-AM^{2}}=\sqrt{R^{2}-\left(\frac{a}{\sqrt{2}}\right)^{2}}=\frac{\sqrt{2R^{2}-a^{2}}}{\sqrt{2}}.
Если точка O
лежит на отрезке PM
, то OM+OP=PM
, или
\frac{\sqrt{2R^{2}-a^{2}}}{\sqrt{2}}+R=\frac{\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}.
Решим полученное уравнение:
\frac{\sqrt{2R^{2}-a^{2}}}{\sqrt{2}}+R=\frac{\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}~\Leftrightarrow~\frac{\sqrt{2R^{2}-a^{2}}}{\sqrt{2}}=\frac{\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}-R~\Leftrightarrow
\Leftrightarrow~R^{2}-\frac{a^{2}}{2}=b^{2}-\frac{a^{2}}{2}-\frac{2R\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}+R^{2}~\Leftrightarrow
\Leftrightarrow~\frac{2R\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}=b^{2}~\Leftrightarrow~R=\frac{b^{2}\sqrt{2}}{2\sqrt{2b^{2}-a^{2}}}.
Возможен также случай, когда точка O
лежит на продолжении высоты PM
за точку M
. Тогда OP=OM+MP
, или
R=\frac{\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}+\frac{\sqrt{2R^{2}-a^{2}}}{\sqrt{2}},
откуда
R=\frac{b^{2}\sqrt{2}}{2\sqrt{2b^{2}-a^{2}}}.
Третий способ. Пусть PM
— высота правильной четырёхугольной пирамиды PABCD
, R
— искомый радиус (рис. 1). Поскольку пирамида правильная, центр её описанной сферы лежит на прямой PM
. Рассмотрим сечение пирамиды плоскостью, проходящей через прямую PM
и точку A
(рис. 2). Получим окружность радиуса R
с центром на прямой PM
, проходящую через точки P
, A
и C
. Тогда R
— радиус окружности, описанной около равнобедренного треугольника APC
.
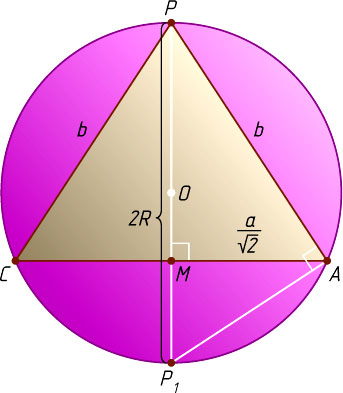
Продолжим PM
до пересечения с окружностью в точке P_{1}
(рис. 2). Тогда \angle PAP_{1}=90^{\circ}
, поэтому PM\cdot MP_{1}=MA^{2}
, или
\frac{\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}\cdot\left(2R-\frac{\sqrt{2b^{2}-a^{2}}}{\sqrt{2}}\right)=\frac{a^{2}}{2}.
Отсюда находим, что
R=\frac{b^{2}\sqrt{2}}{2\sqrt{2b^{2}-a^{2}}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 4(а), с. 88



