8364. Сторона основания правильной треугольной пирамиды равна a
, боковое ребро равно b
. Найдите радиус вписанного шара.
Ответ. \frac{a\sqrt{3}\sqrt{3b^{2}-a^{2}}}{3(a+\sqrt{3}\sqrt{4b^{2}-a^{2}})}
.
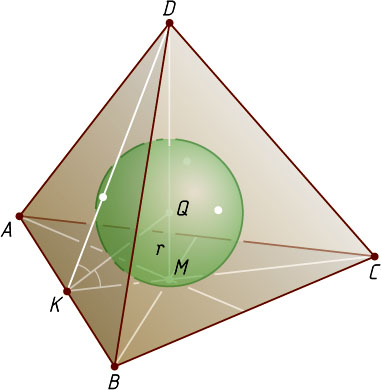
Решение. Пусть DM
— высота правильной треугольной пирамиды ABCD
, r
— искомый радиус. Поскольку пирамида правильная, центр Q
её вписанной сферы лежит на прямой DM
, точки касания сферы с боковыми гранями лежат на апофемах, а точка касания сферы с основанием совпадает с точкой M
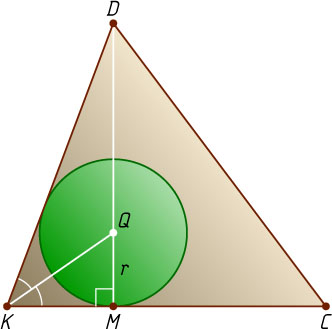
(рис. 1). Рассмотрим сечение пирамиды плоскостью, проходящей через прямую DM
и точку C
(рис. 2). Получим треугольник DKC
(K
— середина AB
) и окружность радиуса r
с центром на высоте DM
, вписанную в угол DKC
. Центр Q
этой окружности лежит на биссектрисе угла DKM
треугольника DKM
, а QM=r
.
Из прямоугольных треугольников DMC
и DKA
находим, что
DM=\sqrt{CD^{2}-CM^{2}}=\sqrt{b^{2}-\left(\frac{a}{\sqrt{3}}\right)^{2}}=\frac{\sqrt{3b^{2}-a^{2}}}{\sqrt{3}},
DK=\sqrt{AD^{2}-AK^{2}}=\sqrt{b^{2}-\left(\frac{a}{2}\right)^{2}}=\frac{\sqrt{4b^{2}-a^{2}}}{2}.
По свойству биссектрисы треугольника \frac{QM}{QD}=\frac{KM}{KD}
, поэтому
\frac{QM}{DM}=\frac{KM}{KM+KD}.
Следовательно,
r=QM=DM\cdot\frac{KM}{KM+KD}=\frac{\sqrt{3b^{2}-a^{2}}}{\sqrt{3}}\cdot\frac{\frac{a}{2\sqrt{3}}}{\frac{a}{2\sqrt{3}}+\frac{\sqrt{4b^{2}-a^{2}}}{2}}=
=\frac{a\sqrt{3}\sqrt{3b^{2}-a^{2}}}{3(a+\sqrt{3}\sqrt{4b^{2}-a^{2}})}
