8370. Сторона основания правильной треугольной пирамиды равна a
, боковое ребро равно b
. Найдите радиус шара, касающегося сторон основания и продолжений боковых рёбер пирамиды.
Ответ. \frac{a(2b+a)}{2\sqrt{3b^{2}-a^{2}}}
.
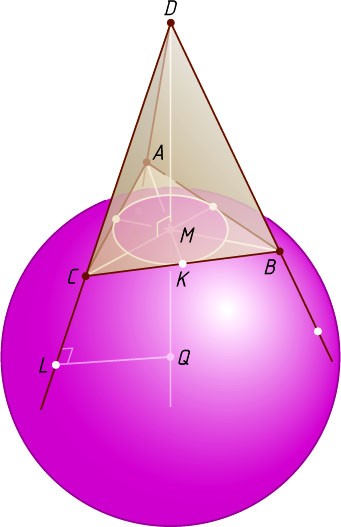
Решение. Пусть DM
— высота правильной треугольной пирамиды ABCD
, r
— искомый радиус. Поскольку пирамида правильная, центр Q
сферы, касающейся сторон основания и продолжений боковых рёбер, лежит на прямой DM
, а точки касания сферы со сторонами основания совпадают с серединами этих сторон. Если K
и L
— точки касания сферы соответственно с ребром BC
и продолжением ребра DC
за точку C
, то
QL\perp CD,~CK=\frac{a}{2},~DL=CD+CL=b+\frac{a}{2}=\frac{2b+a}{2}.
Из прямоугольного треугольника DMC
находим, что
DM=\sqrt{CD^{2}-CM^{2}}=\sqrt{b^{2}-\left(\frac{a}{\sqrt{3}}\right)^{2}}=\frac{\sqrt{3b^{2}-a^{2}}}{\sqrt{3}}.
Из подобия прямоугольных треугольников DLQ
и DMC
следует, что \frac{QL}{DL}=\frac{CM}{DM}
. Значит,
r=QL=DL\cdot\frac{CM}{DM}=\frac{2b+a}{2}\cdot\frac{\frac{a}{\sqrt{3}}}{\frac{\sqrt{3b^{2}-a^{2}}}{\sqrt{3}}}=\frac{a(2b+a)}{2\sqrt{3b^{2}-a^{2}}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 4(г), с. 88
