8376. Найдите радиус сферы, описанной около конуса с радиусом основания r
и высотой h
.
Ответ. \frac{h^{2}+r^{2}}{2h}
.
Решение. Пусть R
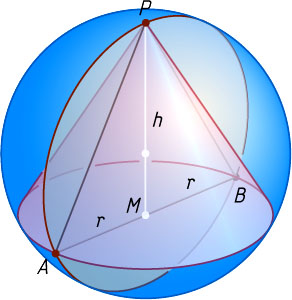
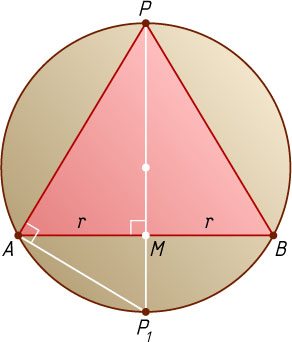
— искомый радиус. Рассмотрим сечение конуса и описанной около него сферы плоскостью, проходящей через высоту PM
конуса (рис. 2). Получим равнобедренный треугольник APB
с основанием AB=2r
и высотой PM=h
и описанную около него окружность радиуса R
. Продолжим PM
за точку M
до пересечения с окружностью в точке P_{1}
. Так как PP_{1}
— диаметр окружности, то треугольник PAP_{1}
— прямоугольный, а AM
— его высота, опущенная ни гипотенузу PP_{1}
. Значит, AM^{2}=PM\cdot P_{1}M
, или r^{2}=h(2R-h)
. Из полученного уравнения находим, что R=\frac{h^{2}+r^{2}}{2h}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5(а), с. 88

