8377. Найдите радиус сферы, вписанной в конус с радиусом основания r
и высотой h
.
Ответ. \frac{hr}{r+\sqrt{h^{2}+r^{2}}}
.
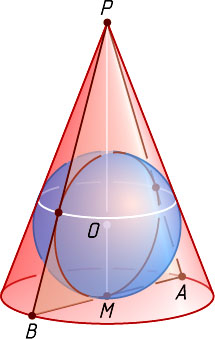
Решение. Пусть R
— искомый радиус, O
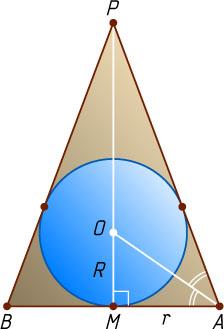
— центр сферы (рис. 1). Рассмотрим сечение конуса и вписанной в него сферы плоскостью, проходящей через высоту PM
конуса (рис. 2). Получим равнобедренный треугольник APB
с основанием AB=2r
и высотой PM=h
и вписанную в него окружность радиуса R
с центром O
. Точка O
лежит на биссектрисе прямоугольного треугольника AMP
, причём OM=R
. По свойству биссектрисы треугольника \frac{OM}{OP}=\frac{AM}{AP}
, или
\frac{R}{h-R}=\frac{r}{\sqrt{h^{2}+r^{2}}}.
Из полученного уравнения находим, что
R=\frac{hr}{r+\sqrt{h^{2}+r^{2}}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5(б), с. 88

