8378. Найдите радиус шара, описанного около правильной n
-угольной призмы с высотой h
и стороной основания a
.
Ответ. \frac{\sqrt{h^{2}\sin^{2}\frac{180^{\circ}}{n}+a^{2}}}{2\sin\frac{180^{\circ}}{n}}
.
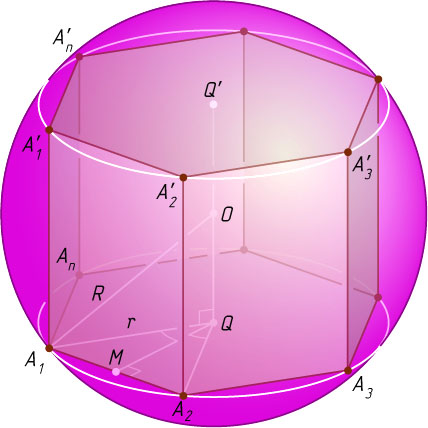
Решение. Центр сферы радиуса R
, описанной около правильной n
-угольной призмы, совпадает с серединой O
отрезка QQ'
, соединяющего центры оснований A_{1}A_{2}\dots A_{n}
и A_{1}'A_{2}'\dots A_{n}'
. Сечение призмы и сферы плоскостью основания A_{1}A_{2}\dots A_{n}
есть правильный многоугольник A_{1}A_{2}\dots A_{n}
, вписанный в окружность радиуса R
с центром в точке Q
.
Пусть r
— радиус этой окружности, M
— середина стороны A_{1}A_{2}
. Из прямоугольных треугольников QMA_{1}
и OQA_{1}
находим, что
r=QA_{1}=\frac{MA_{1}}{\sin\angle MQA_{1}}=\frac{MA_{1}}{\sin\frac{1}{2}\angle A_{1}QA_{2}}=\frac{a}{2\sin\frac{180^{\circ}}{n}},
R=\sqrt{OQ^{2}+QA_{1}^{2}}=\sqrt{\frac{h^{2}}{4}+\frac{a^{2}}{4\sin^{2}\frac{180^{\circ}}{n}}}=\frac{\sqrt{h^{2}\sin^{2}\frac{180^{\circ}}{n}+a^{2}}}{2\sin\frac{180^{\circ}}{n}}.
