8380. Известно, что в некоторую призму можно вписать сферу. Найдите площадь её боковой поверхности, если площадь основания равна S
.
Ответ. 4S
.
Решение. Пусть S_{1}
— площадь боковой поверхности призмы, r
— радиус вписанной сферы, V
— объём призмы. Тогда высота призмы равна 2r
. Поэтому V=2rS
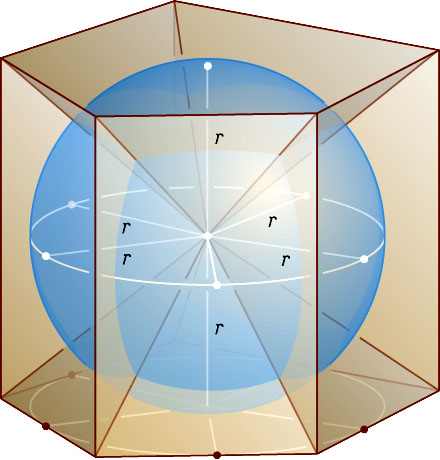
. С другой стороны, соединив центр сферы со всеми вершинами призмы, разобьём призму на пирамиды, вершины которых — центр сферы. Тогда
V=\frac{1}{3}(S_{1}+2S)\cdot r.
Из уравнения 2RS=\frac{1}{3}(S_{1}+2S)\cdot R
находим, что S_{1}=4S
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 8, с. 88
