8381. Плоскость проходит на расстоянии a
от центра единичной сферы. Найдите ребро куба, одна грань которого лежит в этой плоскости, а вершины противоположной грани находятся на сфере.
Ответ. \frac{\sqrt{6-2a^{2}}\pm2a}{3}
.
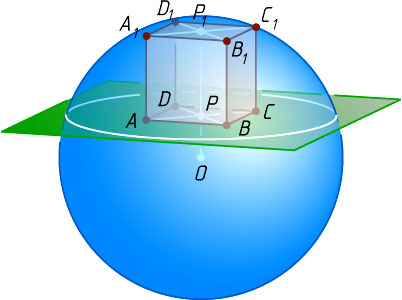
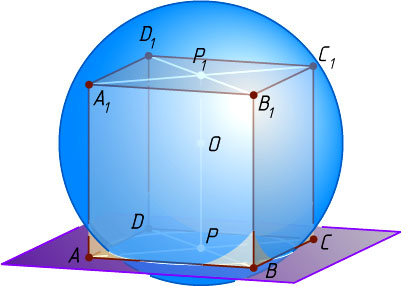
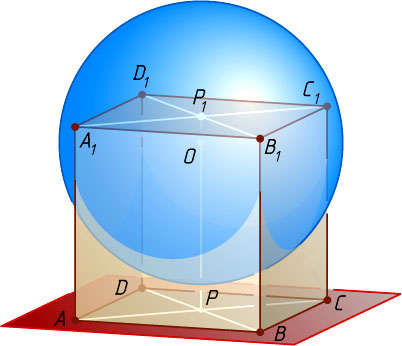
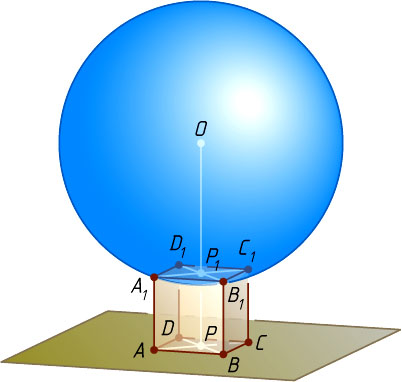
Решение. Пусть вершины A
, B
, C
и D
куба ABCDA_{1}B_{1}C_{1}D_{1}
с ребром x
(рис. 1) лежат в данной плоскости, а вершины A_{1}
, B_{1}
, C_{1}
и D_{1}
на данной сфере с центром O
. Через точку O
проведём прямую, перпендикулярную данной плоскости. Пусть эта прямая пересекает плоскости граней ABCD
и A_{1}B_{1}C_{1}D_{1}
в точках P
и P_{1}
соответственно. Поскольку точки A_{1}
, B_{1}
, C_{1}
и D_{1}
равноудалены от точки O
, точка P_{1}
— центр квадрата A_{1}B_{1}C_{1}D_{1}
. Тогда P
— центр квадрата ABCD
.
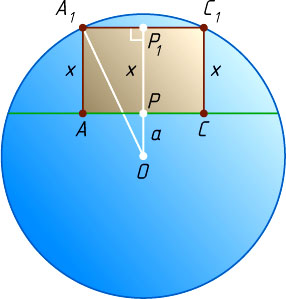
Рассмотрим сечение сферы и куба плоскостью, проходящей через прямую OP
и вершину A_{1}
. Получим окружность единичного радиуса с центром в точке O
и прямоугольник AA_{1}C_{1}C
, сторона AC
которого лежит на хорде окружности, удалённой на расстояние a
от центра окружности, а вершины A_{1}
и C_{1}
— на окружности, причём AA_{1}=x
, а A_{1}C_{1}=x\sqrt{2}
.
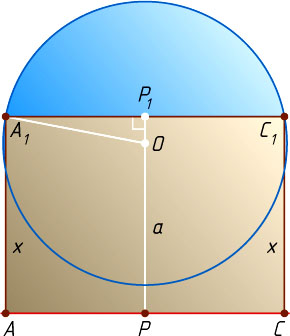
Пусть точки P
и P_{1}
лежат по одну сторону от прямой AC
(рис. 2). Тогда в прямоугольном треугольнике OP_{1}A_{1}
известно, что
OA_{1}=1,~A_{1}P_{1}=\frac{1}{2}A_{1}C_{1}=\frac{x\sqrt{2}}{2},~OP_{1}=OP+PP_{1}=a+x.
По теореме Пифагора OA_{1}^{2}=A_{1}P_{1}^{2}+OP_{1}^{2}
, или
1=\frac{x^{2}}{2}+(a+x)^{2}.
Из этого уравнения находим, что
x=\frac{\sqrt{6-2a^{2}}-2a}{3}
(второй корень отрицательный).
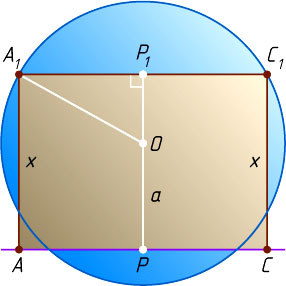
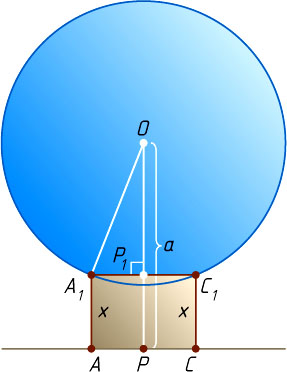
Пусть точки P
и P_{1}
лежат по разные стороны от прямой AC
(рис. 3). Тогда в прямоугольном треугольнике OP_{1}A_{1}
известно, что
OA_{1}=1,~A_{1}P_{1}=\frac{1}{2}A_{1}C_{1}=\frac{x\sqrt{2}}{2},~OP_{1}=PP_{1}-OP=x-a.
По теореме Пифагора OA_{1}^{2}=A_{1}P_{1}^{2}+OP_{1}^{2}
, или
1=\frac{x^{2}}{2}+(x-a)^{2}.
Из этого уравнения находим, что
x=\frac{\sqrt{6-2a^{2}}+2a}{3}
(второй корень отрицательный).
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 10, с. 88







