8382. Известно, что около некоторой призмы можно описать сферу. Докажите, что основание призмы — многоугольник, около которого можно описать окружность. Найдите радиус этой окружности, если высота призмы равна h
, а радиус описанной около неё сферы равен R
.
Ответ. \sqrt{R^{2}-\frac{h^{2}}{4}}
.
Решение. Рассмотрим сечение данных сферы и призмы плоскостью основания призмы. Получим многоугольник основания, вписанный в некоторую окружность.
Рассмотрим сечение сферы и призмы плоскостью боковой грани призмы. Получим параллелограмм, вписанный в окружность, т. е. прямоугольник. Значит, боковые рёбра призмы перпендикулярны плоскости её основания. Следовательно, данная призма — прямая.
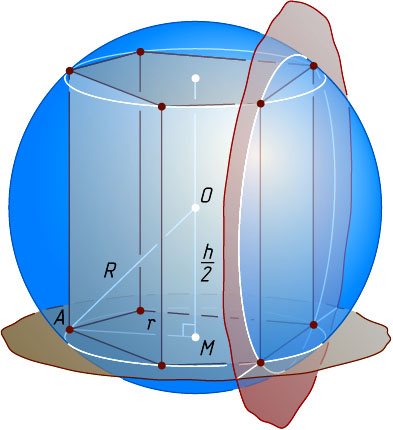
Пусть O
— центр сферы, M
— центр окружности, описанной около одного из оснований, r
— её радиус, A
— вершина этого основания. Тогда
OM=\frac{h}{2},~MA=r,~OA=R.
Из прямоугольного треугольника AOM
находим, что
r=MA=\sqrt{OA^{2}-OM^{2}}=\sqrt{R^{2}-\frac{h^{2}}{4}}.
