8383. Основанием пирамиды служит многоугольник, около которого можно описать окружность. Докажите, что около этой пирамиды можно описать сферу. Найдите радиус этой сферы, если радиус окружности, описанной около основания пирамиды равен r
, высота равна h
, а основание высоты совпадает с вершиной основания пирамиды.
Ответ. \sqrt{r^{2}+\frac{h^{2}}{4}}
.
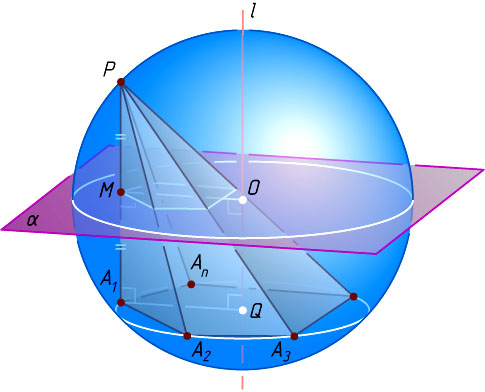
Решение. Пусть Q
— центр окружности, описанной около основания A_{1}A_{2}\dots A_{n}
пирамиды PA_{1}A_{2}\dots A_{n}
с вершиной P
. Геометрическое место точек, равноудалённых от вершин основания пирамиды, есть перпендикуляр l
к плоскости основания, проведённый через точку Q
.
Геометрическое место точек, равноудалённых от вершин A_{1}
и P
, есть плоскость \alpha
, проходящая через середину M
отрезка A_{1}P
перпендикулярно A_{1}P
. Прямая l
и плоскость \alpha
пересекаются, так как в противном случае точка P
лежала бы в плоскости основания пирамиды, что невозможно. Точка O
пересечения прямой l
и плоскости \alpha
равноудалена от всех вершин пирамиды PA_{1}A_{2}\dots A_{n}
. Следовательно, O
— центр сферы, описанной около пирамиды.
Пусть R
— радиус этой сферы, PA_{1}=h
— высота пирамиды. Так как прямые l
и PA_{1}
перпендикулярны к плоскости основания, то l\parallel PA_{1}
. Проведём плоскость через параллельные прямые l
и PA_{1}
. Рассмотрим равнобедренный треугольник A_{1}OP
, в котором OP=OA_{1}=R
, PA_{1}=h
, а высота OM
равна r
(OQA_{1}P
— прямоугольник). Так как M
— середина A_{1}P
, то PM=\frac{h}{2}
. Из прямоугольного треугольника OPM
находим, что
R=OP=\sqrt{OM^{2}+PM^{2}}=\sqrt{r^{2}+\frac{h^{2}}{4}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 12, с. 89
