8385. Найдите ребро куба, одна грань которого принадлежит основанию конуса, а противолежащие ей вершины расположены на боковой поверхности конуса, если радиус основания равен r
, а высота равна h
.
Ответ. \frac{hr\sqrt{2}}{h+r\sqrt{2}}
.
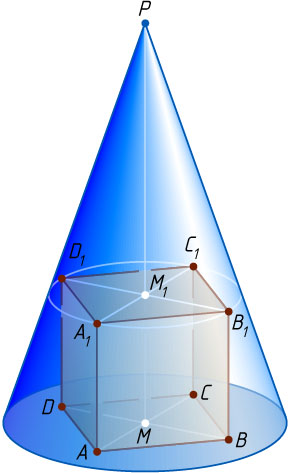
Решение. Пусть вершины A
, B
, C
и D
куба ABCDA_{1}B_{1}C_{1}D_{1}
с ребром x
, лежат на основании конуса с вершиной P
, а вершины A_{1}
, B_{1}
, C_{1}
и D_{1}
— на боковой поверхности конуса (рис. 1).
Так как точки A_{1}
, B_{1}
, C_{1}
и D_{1}
равноудалены от вершины конуса, то высота конуса проходит через центры M
и M_{1}
квадратов ABCD
и A_{1}B_{1}C_{1}D_{1}
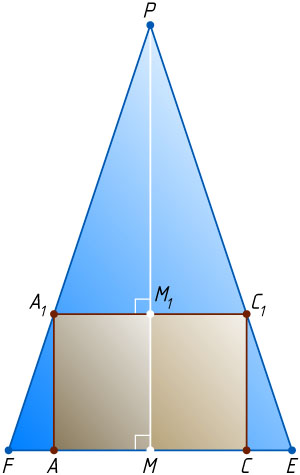
соответственно. Рассмотрим осевое сечение конуса, проходящее через точки A_{1}
и C_{1}
(рис. 2). Получим равнобедренный треугольник PEF
с основанием EF=2r
и высотой PM=h
и вписанный в него прямоугольник AA_{1}C_{1}C
, сторона AC
которого лежит на основании EF
, а вершины A_{1}
и C_{1}
— на боковых сторонах PF
и PE
соответственно. Из подобия треугольников PA_{1}C_{1}
и PFE
следует, что
\frac{PM_{1}}{PM}=\frac{A_{1}C_{1}}{EF},~\mbox{или}~\frac{h-x}{h}=\frac{x\sqrt{2}}{2r}.
Из этого уравнение находим, что
x=\frac{hr\sqrt{2}}{h+r\sqrt{2}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 14, с. 89

