8386. Через центр сферы радиуса R
проведены три попарно перпендикулярные плоскости. Найдите радиус сферы, касающейся всех этих плоскостей и данной сферы.
Ответ. \frac{(\sqrt{3}\pm1)R}{2}
.
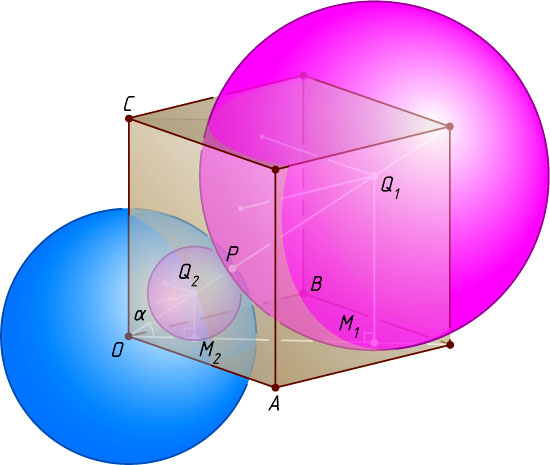
Решение. Пусть указанные плоскости пересекаются по прямым OA
, OB
и OC
, где O
— центр данной сферы радиуса R
. Будем считать, что OA=OB=OC=1
. Если Q
— центр сферы радиуса x
, касающейся данной сферы в точке P
, а также касающейся плоскостей AOB
, AOC
и BOC
, причём плоскости AOB
— в точке M
, то QM\perp OM
, и OQ=OP+QP
(внешнее касание) или OQ=OP-QP
(внутреннее касание).
Обозначим \angle QOM=\alpha
. В прямоугольном треугольнике QOM
имеем соотношение QM=OQ\sin\alpha
, или x=(R\pm x)\sin\alpha
. Таким образом, для решения задачи достаточно найти \sin\alpha
. Для этого рассмотрим куб с вершиной L
. Его диагональ, проведённая из вершины L
, образует с плоскостями трёх граней, содержащих вершину L
, угол, также равный \alpha
. Если ребро куба равно c
, то его диагональ равна c\sqrt{3}
. Значит,
\sin\alpha=\frac{c}{c\sqrt{3}}=\frac{1}{\sqrt{3}}.
Из уравнения x=\frac{R\pm x}{\sqrt{3}}
, находим, что x=\frac{(\sqrt{3}\pm1)R}{2}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 15, с. 89
