8387. Осевым сечением конуса является правильный треугольник со стороной a
. Через ось конуса проведены две перпендикулярные плоскости, которые делят конус на четыре части. Найдите радиус сферы, вписанной в одну из этих частей.
Ответ. \frac{a(\sqrt{3}-\sqrt{2})}{2}
.
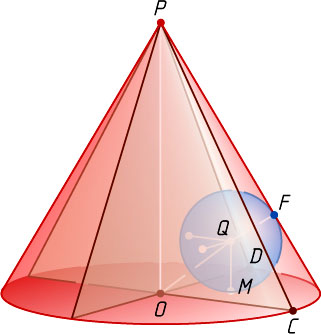
Решение. Пусть P
— вершина конуса, O
— центр основания, r
— радиус сферы с центром Q
, касающейся указанных попарно перпендикулярных плоскостей и боковой поверхности конуса, причём плоскости COD
основания конуса — в точке M
, а боковой поверхности конуса — в точке F
. Можно считать, что OC=OD=OP=\frac{a\sqrt{3}}{2}
.
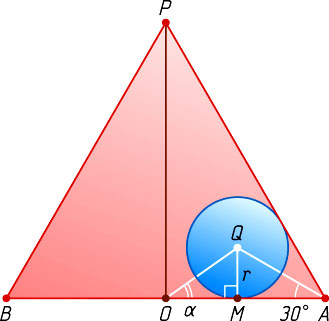
Через высоту PO
конуса и параллельную ей прямую QM
проведём плоскость. Получим осевое сечение конуса — равносторонний треугольник APB
со стороной a
(рис. 2). Окружность радиуса r
с центром Q
вписана в угол PAO
, поэтому
AM=QM\ctg\angle MAQ=r\ctg30^{\circ}=r\sqrt{3}.
Пусть прямая OQ
образует с плоскостью основания конуса угол \alpha
. Тогда
OM=QM\ctg\angle MOQ=r\ctg\alpha.
Поскольку OA=AM+OM
, имеем уравнение \frac{a}{2}=r\sqrt{3}+r\ctg\alpha
. Таким образом, для решения задачи достаточно найти \ctg\alpha
.
Рассмотрим куб с вершиной L
. Его диагональ, проведённая из вершины L
, образует с плоскостями трёх граней, содержащих вершину L
, угол, также равный \alpha
. Если ребро куба равно c
, то его диагональ равна c\sqrt{3}
, а диагональ грани — c\sqrt{2}
. Значит,
\ctg\alpha=\frac{c\sqrt{2}}{c}=\sqrt{2}.
Из уравнения \frac{a}{2}=r\sqrt{3}+r\sqrt{2}
находим, что r=\frac{a(\sqrt{3}-\sqrt{2})}{2}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 16, с. 89

