8389. Два шара касаются друг друга и граней трёхгранного угла, все плоские углы которого прямые. Найдите отношение радиусов этих шаров.
Ответ. 2-\sqrt{3}
.
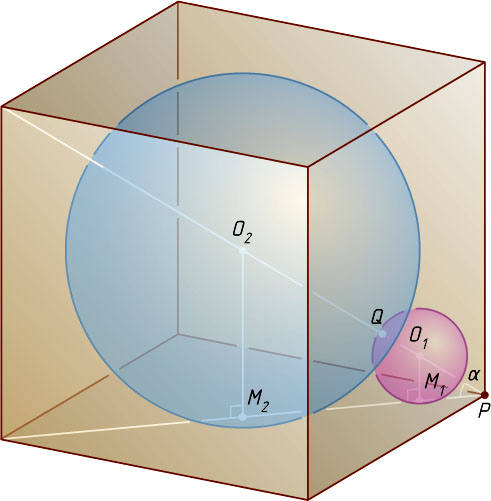
Решение. Рассмотрим куб с вершиной P
(рис. 1). Пусть его диагональ, проведённая из вершины P
, образует с плоскостями трёх граней, содержащих вершину P
, углы, равные \alpha
. Если ребро куба равно c
, то его диагональ равна c\sqrt{3}
. Значит,
\sin\alpha=\frac{c}{c\sqrt{3}}=\frac{1}{\sqrt{3}}.
Пусть касающиеся шары радиусов r
и R
(r\lt R)
с центрами O_{1}
, O_{2}
вписаны в трёхгранный угол с вершиной P
некоторого куба, M_{1}
и M_{2}
— точки касания шаров с плоскостью какой-нибудь грани трёхгранного угла, Q
— точка касания шаров. Тогда O_{1}M_{1}
и O_{2}M_{2}
— перпендикуляры к этой плоскости, точка Q
лежит на отрезке O_{1}O_{2}
, прямая O_{1}O_{2}
образует с этой плоскостью угол \alpha
.
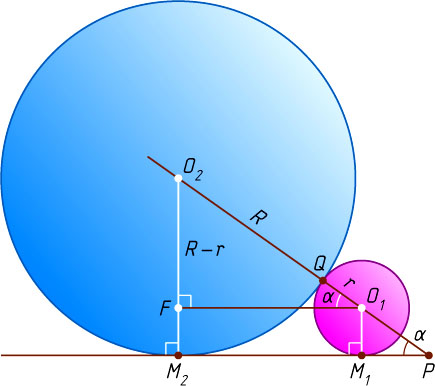
Проведём плоскость через параллельные прямые O_{1}M_{1}
и O_{2}M_{2}
(рис. 2). Опустим перпендикуляр O_{1}F
из центра O_{1}
меньшего шара на прямую O_{2}M_{2}
. В прямоугольном треугольнике O_{1}FO_{2}
известно, что
O_{1}O_{2}=r+R,~O_{2}F=R-r,~\angle FO_{1}O_{2}=\alpha.
Поэтому
\frac{R-r}{R+r}=\frac{O_{2}F}{O_{1}O_{2}}=\sin\angle FO_{1}O_{2}=\sin\alpha=\frac{1}{\sqrt{3}}.
Тогда
(R-r)\sqrt{3}=R+r,~R(\sqrt{3}-1)=r(\sqrt{3}+1).
Следовательно,
\frac{r}{R}=\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 18, с. 89

