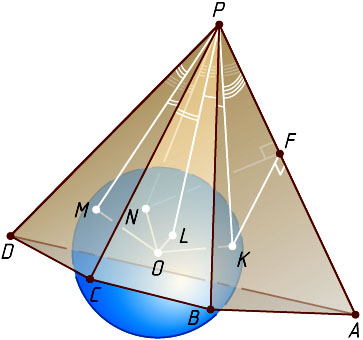
8390. Докажите, что если в четырёхгранный угол можно вписать сферу, то суммы противоположных плоских углов этого четырёхгранного угла равны.
Решение. Пусть сфера с центром O
касается граней APB
, BPC
, CPD
и APD
четырёхгранного угла PABCD
с вершиной P
в точках K
, L
, M
и N
соответственно. Пусть плоскость \alpha
, проведённая через пересекающиеся прямые OK
и ON
, пересекает ребро AP
в точке F
. Прямая AP
перпендикулярна плоскости \alpha
, так как она перпендикулярна двум пересекающимся прямым OK
и OL
этой плоскости. Тогда KF\perp AP
и NF\perp AP
. Прямоугольные треугольники PFK
и PFN
равны по катету и гипотенузе. Значит, \angle APK=\angle APN
. Аналогично,
\angle BPK=\angle BPL,~\angle CPL=\angle CPM,~\angle DPM=\angle DPN.
Следовательно,
\angle APB+\angle CPD=(\angle APK+\angle BPK)+(\angle CPM+\angle DPM)=
=(\angle APN+\angle BPL)+(\angle CPL+\angle DPN)=
=(\angle BPL+\angle CPL)+(\angle APN+\angle DPN)=\angle BPC+\angle APD.
Что и требовалось доказать.
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 5.21, с. 84
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 6.26, с. 79
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 20(а), с. 89
