8402. Две противоположные вершины единичного куба совпадают с центрами оснований цилиндра, а остальные вершины расположены на боковой поверхности цилиндра. Найдите высоту и радиус основания цилиндра.
Ответ. \sqrt{3}
, \frac{\sqrt{6}}{3}
.
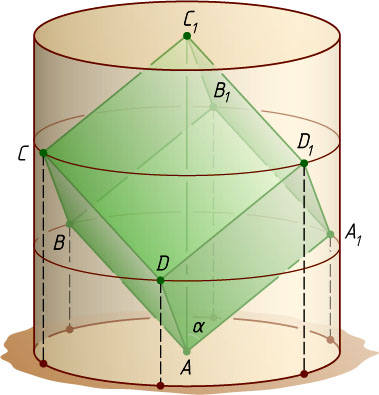
Решение. Пусть противоположные вершины A
и C_{1}
куба ABCDA_{1}B_{1}C_{1}D_{1}
совпадают с центрами оснований цилиндра с высотой h
и радиусом основания r
, а остальные вершины куба расположены на боковой поверхности цилиндра (рис. 1). Тогда h=AC_{1}=\sqrt{3}
.
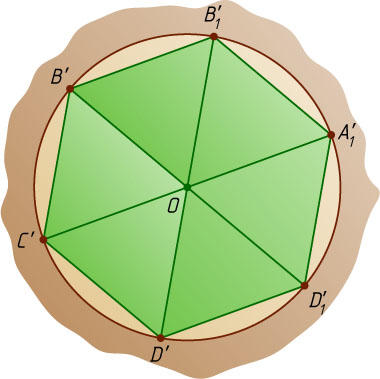
При ортогональном проектировании данных куба и цилиндра на плоскость, перпендикулярную прямой AC_{1}
, боковая поверхность перейдёт в окружность радиуса r
, точки A
и C_{1}
перейдут в центр O
этой окружности, точки B
, C
, D
, A_{1}
, B_{1}
и D_{1}
— соответственно в точки B'
, C'
, D'
, A_{1}'
, B_{1}'
и D_{1}'
, лежащие на окружности, причём B'C'D'D_{1}'A_{1}'B_{1}'
— правильный шестиугольник с центром O
. Радиус основания цилиндра равен стороне этого шестиугольника.
Обозначим \angle A_{1}AC_{1}=\alpha
. Из прямоугольного треугольника A_{1}AC_{1}
находим, что
\sin\alpha=\sin\angle A_{1}AC_{1}=\frac{A_{1}C_{1}}{AC_{1}}=\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}.
Так как прямая AC_{1}
перпендикулярна плоскости основания цилиндра, то угол между прямой AA_{1}
и плоскостью основания цилиндра равен 90^{\circ}-\alpha
. Следовательно,
r=OA_{1}'=AA_{1}\cos(90^{\circ}-\alpha)=AA_{1}\sin\alpha=\frac{\sqrt{2}}{\sqrt{3}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 1, с. 95
Источник: Понарин Я. П. Элементарная геометрия. — Т. 2: Стереометрия. — М.: МЦНМО, 2006. — № 12, с. 238

