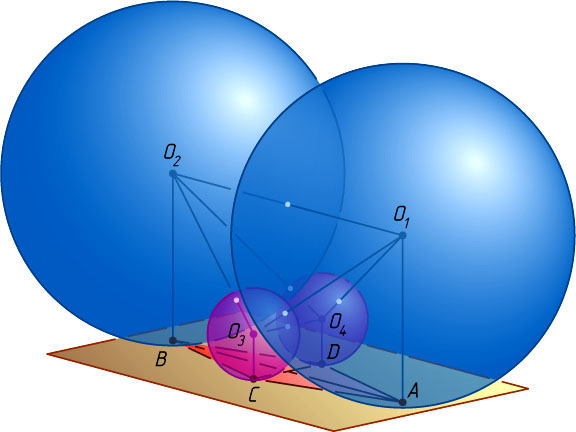
8439. Два шара одного радиуса и два — другого расположены так, что каждый шар касается трёх других и одной плоскости. Найдите отношение радиуса большего шара к радиусу меньшего.
Ответ. 2+\sqrt{3}
.
Решение. Пусть O_{1}
и O_{2}
— центры больших шаров радиуса R
, A
и B
— их точки касания с данной плоскостью; O_{3}
и O_{4}
— центры меньших шаров радиуса r
; C
и D
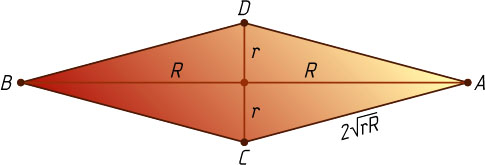
— их точки касания с данной плоскостью. Тогда ACBD
— ромб (рис. 1) со стороной 2\sqrt{rR}
(рис. 2) и диагоналями 2r
и 2R
(см. задачу 365). Поэтому AC=\sqrt{r^{2}+R^{2}}
. Из уравнения
2\sqrt{rR}=\sqrt{r^{2}+R^{2}}
находим, что \frac{R}{r}=2\pm\sqrt{3}
. Так как \frac{R}{r}\gt1
, то искомое отношение равно 2+\sqrt{3}
.
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 4.3, с. 62
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 7, с. 110

