8691. В прямоугольном параллелепипеде проведена плоскость, которая проходит через его диагональ, образует углы 45^{\circ}
и 30^{\circ}
со сторонами основания и параллельна диагонали основания параллелепипеда. Чему равна площадь поверхности сферы, описанной около параллелепипеда, если расстояние от этой плоскости до диагонали основания равно l
?
Ответ. 22\pi l^{2}
.
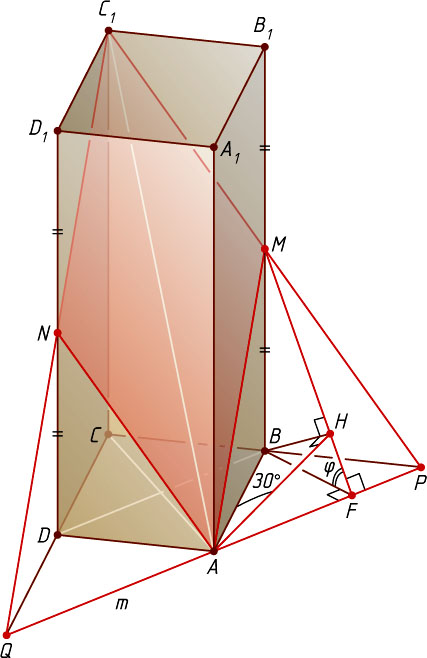
Решение. Пусть плоскость \alpha
проходит через диагональ AC_{1}
параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
параллельно диагонали BD
основания ABCD
.
Плоскость основания ABCD
проходит через прямую BD
, параллельную секущей плоскости \alpha
, поэтому прямая m
пересечения плоскости \alpha
с плоскостью этого основания параллельна прямой BD
. Пусть прямая m
пересекает прямые BC
и CD
в точках P
и Q
соответственно. Тогда PB=AD
как противоположные стороны параллелограмма ADBP
.
Если прямые C_{1}Q
и DD_{1}
пересекаются в точке N
, а прямые C_{1}P
и BB_{1}
— в точке M
, то плоскость \alpha
пересекает параллелепипед по параллелограмму AMC_{1}N
. Из равенства треугольников BMP
и B_{1}MC_{1}
(по стороне и двум прилежащим к ней углам) следует, что M
— середина ребра BB_{1}
. Аналогично, N
— середина ребра DD_{1}
.
Пусть F
— основание перпендикуляра, опущенного из точки B
на прямую PQ
, а H
— основание перпендикуляра, опущенного из точки B
на прямую MF
. Тогда BH
— перпендикуляр к плоскости \alpha
. Из условия задачи следует, что BH=l
(поскольку прямая BD
параллельна плоскости \alpha
, то расстояния от каждой точки этой прямой до плоскости \alpha
равны l
). Кроме того, HAB
— угол бокового ребра AB
с плоскостью \alpha
. По условию задачи \angle HAB=30^{\circ}
. Из прямоугольного треугольника HAB
находим, что AB=2BH=2l
.
Рассуждая аналогично, найдём, что AD=\frac{l}{\cos45^{\circ}}=l\sqrt{2}
.
Рассмотрим прямоугольный треугольник ABP
. В нём
AB=2l,~PB=AD=l\sqrt{2},~AP=\sqrt{4l^{2}+2l^{2}}=l\sqrt{6},
BF=\frac{AB\cdot BP}{AP}=\frac{2l\cdot l\sqrt{2}}{l\sqrt{6}}=\frac{2l}{\sqrt{3}}.
Обозначим \angle MFB=\varphi
. Из прямоугольного треугольника BHF
находим, что
\sin\varphi=\frac{BH}{BF}=\frac{l}{\frac{2l}{\sqrt{3}}}=\frac{\sqrt{3}}{2},
а так как \varphi\lt90^{\circ}
, то \varphi=60^{\circ}
. Из прямоугольного треугольника MBF
находим, что
MB=BF\tg\varphi=\frac{2l}{\sqrt{3}}\cdot\sqrt{3}=2l.
Тогда BB_{1}=2BM=4l
.
Пусть R
— радиус сферы, описанной около параллелепипеда. Поскольку диагональ прямоугольного параллелепипеда есть диаметр этой сферы, а квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений,
4R^{2}=AB^{2}+AD^{2}+BB_{1}^{2}=4l^{2}+2l^{2}+16l^{2}=22l^{2}.
Следовательно, если S
— площадь поверхности сферы, то S=4\pi R^{2}=22\pi l^{2}
.
Источник: Вступительный экзамен в МГТУ им. Н. Э. Баумана. — 2002, № 7, вариант 1
