8692. Найдите площадь сечения правильной треугольной призмы ABCA_{1}B_{1}C_{1}
плоскостью, проходящей через вершину C
и середину стороны B_{1}C_{1}
основания A_{1}B_{1}C_{1}
и параллельной диагонали AC_{1}
боковой грани AA_{1}C_{1}C
, если расстояние между прямой AC_{1}
и секущей плоскостью равно 1, а сторона основания призмы равна \sqrt{14}
.
Ответ. \frac{21}{4}
.
Решение. Обозначим через a
сторону основания призмы (a=\sqrt{14}
). Плоскость боковой грани AA_{1}C_{1}C
проходит через прямую AC_{1}
, параллельную секущей плоскости, и имеет с ней общую точку C
, поэтому прямая l
пересечения этих плоскостей параллельна прямой AC_{1}
. Пусть прямая l
пересекается с прямыми A_{1}C_{1}
и AA_{1}
в точках P
и Q
соответственно. Тогда C_{1}P=AC=A_{1}C_{1}=a
как противоположные стороны параллелограмма ACPC_{1}
. Аналогично AQ=CC_{1}=AA_{1}
. Значит, AC_{1}
— средняя линия треугольника PA_{1}Q
.
Пусть M
— середина B_{1}C_{1}
, а прямая PM
пересекает ребро A_{1}B_{1}
в точке N
. Через вершину B_{1}
проведём прямую, параллельную A_{1}C_{1}
, и продолжим PM
до пересечения с этой прямой в точке T
. Из равенства треугольников TMB_{1}
и PMC_{1}
следует, что TB_{1}=PC_{1}=a
, а из подобия треугольников TNB_{1}
и PNA_{1}
— \frac{B_{1}N}{NA_{1}}=\frac{TB_{1}}{PA_{1}}=\frac{1}{2}
.
Пусть прямая NQ
пересекает ребро AB
в точке L
. Тогда AL
— средняя линия треугольника NQA_{1}
, поэтому
AL=\frac{1}{2}A_{1}N=\frac{1}{2}\cdot\frac{2}{3}A_{1}B_{1}=\frac{1}{3}A_{1}B_{1}=\frac{1}{3}AB,
а сечение призмы данной плоскостью — трапеция MNLC
. Найдём площадь ортогональной проекции сечения на плоскость основания ABC
. Пусть N'
и M'
— проекции точек N
и M
на эту плоскость. Тогда M'
— середина BC
, а точка N'
такова, что \frac{BN'}{BA}=\frac{1}{3}
, значит,
S'=S_{LN'M'C}=S_{\triangle BLC}-S_{\triangle BN'M'}=\frac{BL}{BA}S_{\triangle ABC}-\frac{BN'}{BA}\cdot\frac{BM'}{BC}S_{\triangle ABC}=
=\frac{2}{3}S_{\triangle ABC}-\frac{1}{3}\cdot\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}S_{\triangle ABC}=\frac{a^{2}\sqrt{3}}{8}=\frac{7\sqrt{3}}{4}.
Пусть K
— основание перпендикуляра, опущенного из точки C_{1}
на прямую MP
. Тогда по теореме о трёх перпендикулярах CK\perp PM
, причём прямая CK
лежит в секущей плоскости, поэтому CKC_{1}
— линейный угол двугранного угла между секущей плоскостью и плоскостью основания призмы. Обозначим \angle CKC_{1}=\varphi
.
Из треугольника MC_{1}P
по теореме косинусов находим, что
MP=\sqrt{a^{2}+\frac{a^{2}}{4}-2\cdot a\cdot\frac{a}{2}\cdot\cos120^{\circ}}=\frac{a\sqrt{7}}{2}=\frac{7\sqrt{2}}{2}.
Записав площадь треугольника MC_{1}P
двумя способами, получим, что
C_{1}K=\frac{C_{1}P\cdot C_{1}M\sin\angle MC_{1}P}{MP}=\frac{\frac{a}{2}\cdot a\sin120^{\circ}}{\frac{a\sqrt{7}}{2}}=\sqrt{\frac{3}{2}}.
Если C_{1}H
— высота прямоугольного треугольника CC_{1}K
, то расстояние между прямой AC_{1}
и секущей плоскостью равно длине отрезка C_{1}H
, т. е. C_{1}H=1
. Из прямоугольного треугольника CC_{1}K
находим, что
\sin\varphi=\frac{C_{1}H}{C_{1}K}=\frac{1}{\sqrt{\frac{3}{2}}}=\sqrt{\frac{2}{3}},~\cos\varphi=\frac{1}{\sqrt{3}}.
Следовательно, если S
— искомая площадь сечения, то
S=\frac{S'}{\cos\varphi}=\frac{\frac{7\sqrt{3}}{4}}{\frac{1}{\sqrt{3}}}=\frac{21}{4}.
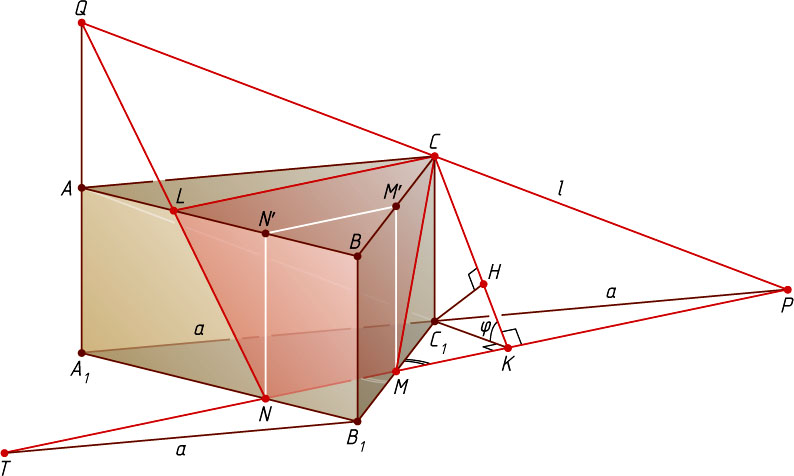
Источник: Вступительный экзамен в МГТУ им. Н. Э. Баумана. — 2002, № 7, вариант 2
