8693. В правильную треугольную пирамиду SABC
с основанием ABC
вписан шар, к нему проведена касательная плоскость, параллельная грани ASC
. Эта плоскость пересекает ребро SB
в точке M
, причём BM:MS=1{,}55
. Найдите косинус угла между боковой гранью и плоскостью основания пирамиды.
Ответ. \frac{7}{10}
.
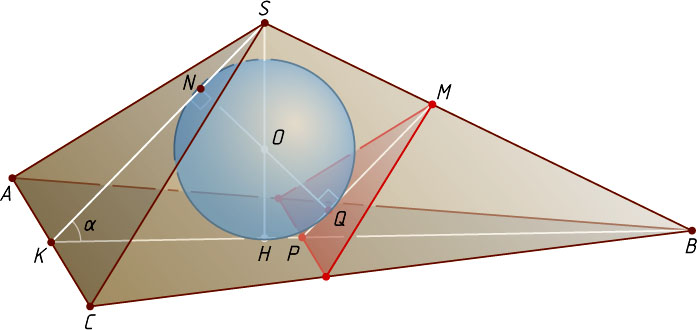
Решение. Поскольку пирамида правильная, центр O
её вписанного шара лежит на высоте SH
(рис. 1), точка N
касания шара с плоскостью грани ASC
лежит на апофеме SK
(K
— середина AC
), точка касания шара с плоскостью основания пирамиды совпадает с точкой H
, а точка Q
касания шара с секущей плоскостью лежит на прямой, проходящей через точку M
параллельно апофеме SK
.
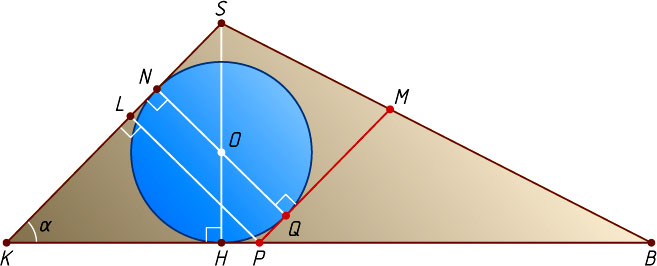
Рассмотрим сечение пирамиды плоскостью BKS
(рис. 2). Прямая MQ
пересекает медиану BK
треугольника ABC
в точке P
. Обозначим BK=a
. Тогда
\frac{BP}{PK}=\frac{BM}{MS}=1{,}55,~\frac{KP}{BK}=\frac{SM}{BS}=\frac{SM}{SM+BM}=\frac{1}{1+1{,}55}=\frac{1}{2{,}55}=\frac{100}{255}=\frac{20}{51},
KP=\frac{20}{51}BK=\frac{20}{51}a,~KH=\frac{1}{3}BK=\frac{1}{3}a=\frac{17}{51}a,
PQ=PH=KP-KH=\frac{20}{51}a-\frac{1}{3}a=\frac{1}{17}a,KN=KH=\frac{17}{51}a.
Поскольку OQ\perp PM
и ON\perp SK
(как радиусы, проведённые в точки касания) и MP\parallel SK
, точки N
, O
и Q
лежат на одной прямой. Пусть L
— основание перпендикуляра, опущенного из точки P
на SK
. Если \alpha
— угол боковой грани пирамиды с плоскостью основания, то
\cos\alpha=\cos\angle SKH=\cos\angle LKH=\frac{KL}{KH}=\frac{KN-NL}{KP}=\frac{\frac{17}{51}a-\frac{1}{17}a}{\frac{20}{51}a}=
=\frac{\frac{14}{51}a}{\frac{20}{51}a}=\frac{14}{20}=\frac{7}{10}.
Источник: Вступительный экзамен в МИНХиГП. — 2002, № 12, вариант 1

