8694. Образующая конуса составляет с плоскостью его основания угол \alpha
, \cos\alpha=\frac{1}{4}
. В конус вписан шар, через окружность касания шара и боковой поверхности конуса проведена плоскость. Объём части конуса, заключённой между этой плоскостью и плоскостью основания конуса, равен 37. Найдите объём остальной части конуса.
Ответ. 27.
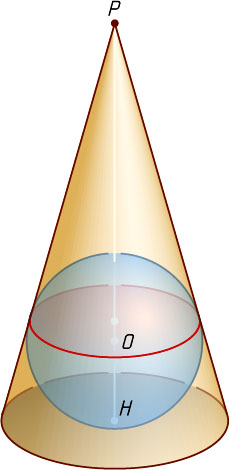
Решение. Пусть P
— вершина конуса, PH
— его высота, O
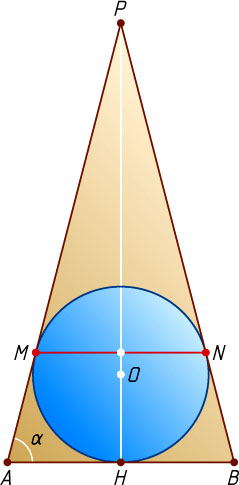
— центр вписанного в него шара. Рассмотрим осевое сечение конуса — равнобедренный треугольник PAB
с углом \alpha
при основании AB
. При этом сечение шара есть окружность с центром O
, вписанная в треугольника PAB
и касающаяся основания AB
в точке H
, а боковых сторон PA
и PB
— в точках M
и N
соответственно.
Пусть K
— середина MN
, R
— радиус основания конуса, V
— его объём, v
— искомый объём. Тогда V-v=37
. Поскольку конус, отсекаемый от данного конуса указанной плоскостью, подобен данному конусу, v=k^{3}V
, где k
— коэффициент подобия. Далее имеем:
k=\frac{PM}{PA}=\frac{PA-AM}{PA}=\frac{PA-AH}{PA}=1-\frac{AH}{PA}=1-\frac{R}{\frac{R}{\cos\alpha}}=1-\cos\alpha=1-\frac{1}{4}=\frac{3}{4},
v=\left(\frac{3}{4}\right)^{3}V=\frac{27}{64}V,~V-v=V-\frac{27}{64}V=\frac{37}{64}V=37,~V=64.
Следовательно, v=\frac{27}{64}V=27
.
Источник: Вступительный экзамен в МИНХиГП. — 2002, № 12, вариант 2

