8695. В пирамиде ABCD
длина отрезка BD
равна \frac{5}{2}
, точка E
— середина AB
, а F
— точка пересечения медиан грани BCD
, причём EF=8
. Сфера радиуса 5 касается плоскостей ABD
и BCD
в точках E
и F
соответственно. Найдите двугранный угол между гранями ABD
и BCD
, площадь грани BCD
и объём пирамиды ABCD
.
Ответ. \arccos\frac{7}{25}=\arcsin\frac{24}{25}
; 25; \frac{320}{3}
.
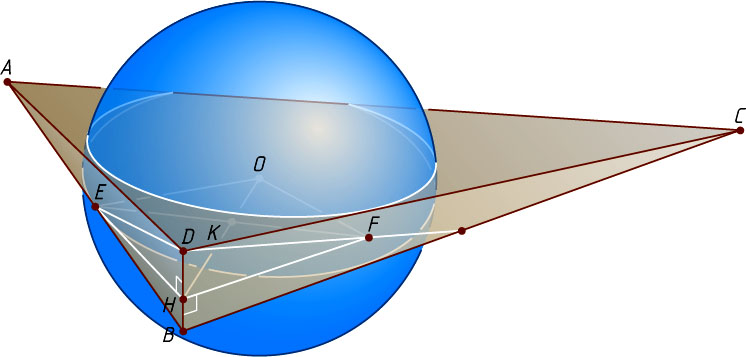
Решение. Пусть O
— центр сферы (рис. 1). Поскольку радиусы OE
и OF
проведены в точки касания сферы с плоскостями ABD
и BCD
, прямая OE
перпендикулярна плоскости ABD
, а прямая OF
— плоскости BCD
, значит, OE\perp BD
и OF\perp BD
, а также OE\perp DE
и OF\perp DF
.
Пусть плоскость, проведённая через пересекающиеся прямые OE
и OF
пересекает прямую BD
в точке H
. Поскольку прямая BD
перпендикулярна пересекающимся прямым OE
и OF
этой плоскости, плоскость OEF
перпендикулярна прямой BD
, значит, EHF
— линейный угол двугранного угла между гранями ABD
и BCD
. Положим \angle EHF=2\alpha
.
Из равенства отрезков DE
и DF
(отрезки касательных, проведённых к сфере из одной точки) следует равенство прямоугольных треугольников EHD
и FHD
(по катету и гипотенузе), значит, EH=FH
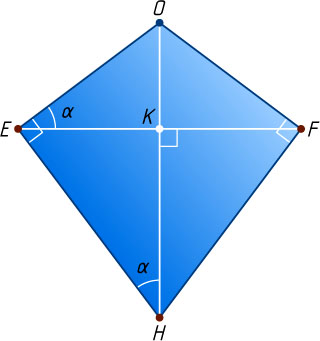
. Таким образом, в четырёхугольнике OEHF
(рис. 2) точки O
и H
равноудалены от концов диагонали EF
, поэтому HO\perp EF
и диагональ OH
проходит через середину K
диагонали EF
. Тогда
\angle OEK=\angle EHO=\frac{1}{2}\angle EHF=\alpha,~\cos\alpha=\frac{EK}{OE}=\frac{4}{5}.
Следовательно,
\cos2\alpha=2\cos^{2}\alpha-1=2\cdot\frac{16}{25}-1=\frac{32}{25}-1=\frac{7}{25}.
Из прямоугольного треугольника треугольника HKF
находим, что
FH=\frac{KF}{\sin\angle KFH}=\frac{KF}{\sin\alpha}=\frac{4}{\sqrt{1-\cos^{2}\alpha}}=\frac{4}{\sqrt{1-\frac{16}{25}}}=\frac{20}{3}.
Поскольку FH\perp BD
, отрезок FH
— высота треугольника DBF
, а так как F
— точка пересечения медиан треугольника BCD
, то
S_{\triangle BDC}=3S_{\triangle BDF}=3\cdot\frac{1}{2}BD\cdot FH=\frac{3}{2}\cdot\frac{5}{2}\cdot\frac{20}{3}=25.
Поскольку EH\perp BD
, отрезок EH
— высота треугольника BED
, а так как E
— середина ребра AB
и EH=FH=\frac{20}{3}
, то
S_{\triangle ABD}=2S_{\triangle BDE}=2\cdot\frac{1}{2}BD\cdot EH=\frac{5}{2}\cdot\frac{20}{3}=\frac{50}{3}.
Воспользуемся формулой V=\frac{2}{3}\cdot\frac{S_{1}\cdot S_{2}\sin\varphi}{a}
, где V
— объём тетраэдра, S_{1}
и S_{2}
— площади двух его граней, \varphi
— угол между этими гранями, a
— длина их общего ребра. В нашем случае
V_{ABCD}=\frac{2}{3}\cdot\frac{S_{ABD}\cdot S_{BCD}\sin2\alpha}{BD}=\frac{2}{3}\cdot\frac{\frac{50}{3}\cdot25\cdot2\cdot\frac{3}{5}\cdot\frac{4}{5}}{\frac{5}{2}}=\frac{320}{3}.
Источник: Вступительный экзамен в МФТИ. — 2004, билет 1, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 04-1-6, с. 426

