8699. Сторона основания ABCD
правильной пирамиды SABCD
равна 2. Плоскость \alpha
, параллельная прямым SC
и AD
, пересекает пирамиду так, что в сечение можно вписать окружность, причём периметр сечения равен \frac{32}{5}
. Найдите:
1) в каком отношении плоскость \alpha
делит рёбра пирамиды;
2) отношение объёмов частей, на которые плоскость \alpha
разбивает пирамиду;
3) расстояние от центра описанной около пирамиды сферы до плоскости \alpha
.
Ответ. \frac{2}{3}
; \frac{26}{99}
; \frac{22\sqrt{14}}{35\sqrt{15}}
.
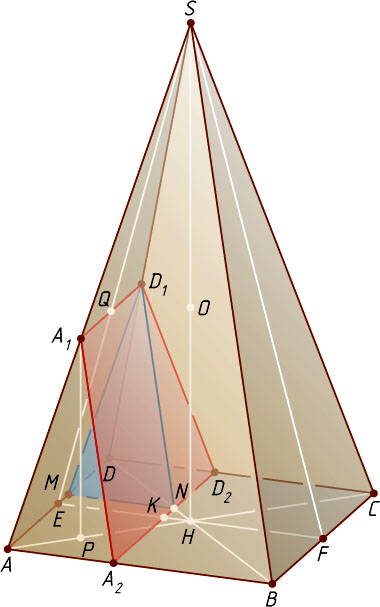
Решение. 1) Через прямую AD
, параллельную плоскости \alpha
, проходит плоскость ASD
, пересекающая плоскость \alpha
по некоторой прямой m
, значит, m\parallel AD
(рис. 1). Пусть A_{1}
и D_{1}
— точки пересечения прямой m
с боковыми рёбрами SA
и SD
соответственно.
Через прямую AD
, параллельную плоскости \alpha
проходит плоскость ABCD
, пересекающая плоскость \alpha
по некоторой прямой l
, значит, l\parallel AD
. Пусть A_{2}
и D_{2}
— точки пересечения прямой l
с рёбрами AB
и CD
соответственно. Тогда A_{2}D_{2}=AD=2
.
Поскольку A_{1}D_{1}\parallel A_{2}D_{2}
, сечение A_{1}A_{2}D_{2}D_{1}
— трапеция, а так как плоскость \alpha
параллельна двум пересекающимся прямым SC
и BC
плоскости BSC
, то плоскости \alpha
и BSC
параллельны, поэтому D_{1}D_{2}\parallel SC
и A_{1}A_{2}\parallel SB
.
Обозначим \frac{DD_{2}}{DC}=\frac{AA_{2}}{AB}=k
, SA=SB=SC=SD=b
. Тогда
A_{1}A_{2}=D_{1}D_{2}=SC\cdot\frac{DD_{2}}{DC}=kb,~A_{1}D_{1}=AD\cdot\frac{SD_{1}}{SD}=(1-k)AD=2(1-k).
Поскольку в трапецию можно вписать окружность, суммы её противоположных сторон равны между собой, значит, сумма её оснований равна половине периметра трапеции, т. е. 2+2(1-k)=\frac{16}{5}
, откуда k=\frac{2}{5}
. Следовательно,
\frac{AA_{2}}{A_{2}B}=\frac{DD_{2}}{D_{2}C}=\frac{DD_{1}}{D_{1}S}=\frac{AA_{1}}{A_{1}S}=\frac{2}{3}.
2) Поскольку сумма боковых сторон A_{1}A_{2}
и D_{1}D_{2}
трапеции A_{1}A_{2}D_{2}D_{1}
также равна полупериметру трапеции, имеем уравнение
2kb=\frac{16}{5},~\mbox{или}~\frac{4}{5}b=\frac{16}{5},
откуда b=4
.
Пусть SH
— высота пирамиды SABCD
. Из прямоугольного треугольника SHA
находим, что
SH=\sqrt{SA^{2}-HA^{2}}=\sqrt{16-2}=\sqrt{14},
Значит,
V_{SABCD}=\frac{1}{3}S_{ABCD}\cdot SH=\frac{1}{3}\cdot4\cdot\sqrt{14}=\frac{4\sqrt{14}}{3}.
Пусть P
— проекция точки A_{1}
на плоскость основания. Тогда точка P
лежит на отрезке AH
. Из подобия треугольников AA_{1}P
и ASH
находим, что
A_{1}P=SH\cdot\frac{AA_{1}}{AS}=\sqrt{14}\cdot\frac{2}{5}=\frac{2\sqrt{14}}{5}.
Пусть плоскость, проходящая через точку D_{1}
параллельно плоскости SAB
пересекает отрезки AD
и A_{2}D_{2}
в точках M
и N
соответственно. Многогранник ADD_{2}A_{2}A_{1}D_{1}
состоит из треугольной призмы AMNA_{2}A_{1}D_{1}
с основаниями AA_{1}A_{2}
, MD_{1}N
и четырёхугольной пирамиды D_{1}MDD_{2}N
с основанием MDD_{2}N
, а так как
AM=A_{1}D=2(1-k)=\frac{6}{5},~MD=AD-MD=2-\frac{6}{5}=\frac{4}{5},~MN=DD_{2}=\frac{4}{5},
то
V_{ADD_{2}A_{2}A_{1}D_{1}}=V_{AMNA_{2}A_{1}D_{1}}+V_{D_{1}MDD_{2}N}=\frac{1}{2}S_{MNA_{2}A}\cdot A_{1}P+\frac{1}{3}S_{MDD_{2}N}\cdot A_{1}P=
=\frac{1}{2}AM\cdot MN\cdot A_{1}P+\frac{1}{3}MD\cdot DD_{2}\cdot A_{1}P=\frac{1}{2}\cdot\frac{6}{5}\cdot\frac{4}{5}\cdot\frac{2\sqrt{14}}{5}+\frac{1}{3}\cdot\frac{4}{5}\cdot\frac{4}{5}\cdot\frac{2\sqrt{2}}{5}=
=\frac{26\cdot4\sqrt{14}}{3\cdot125}.
Тогда
\frac{V_{ADD_{2}A_{2}A_{1}D_{1}}}{V}=\frac{\frac{26\cdot4\sqrt{14}}{3\cdot125}}{\frac{4\sqrt{14}}{3}}=\frac{26}{125}.
Следовательно, отношение объёмов частей, на которые плоскость \alpha
разбивает пирамиду, равно \frac{26}{99}
.
3) Поскольку пирамида правильная, центр O
её описанной сферы лежит на высоте SH
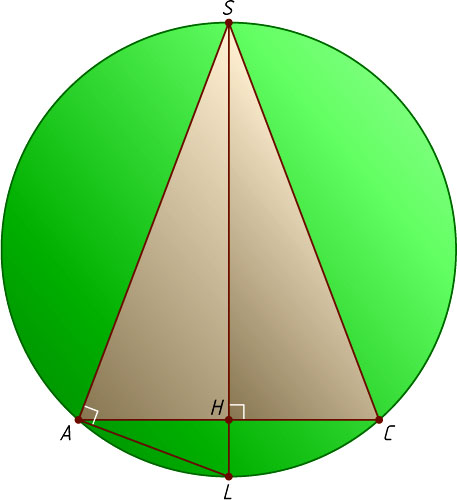
. Рассмотрим сечение пирамиды плоскостью ASC
(рис. 3). Получим равнобедренный треугольник ASC
и описанную около него окружность с центром O
на высоте SH
, причём радиус R
этой окружности равен радиусу сферы. Продолжим SH
до пересечения с окружностью в точке L
. Так как AH
— высота прямоугольного треугольника SAQ
, проведённая из вершины прямого угла, AH^{2}=SH\cdot HL
, или 2=\sqrt{14}(2R-\sqrt{14})
, откуда находим, что R=\frac{8}{\sqrt{14}}
.
Пусть E
и F
— середины AD
и BC
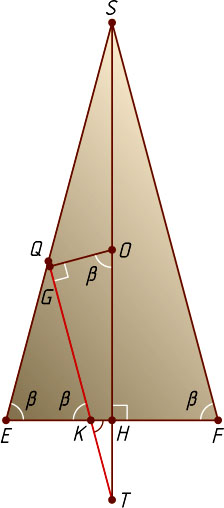
соответственно. Рассмотрим сечение пирамиды плоскостью SEF
. Прямая n
пересечения плоскостей \alpha
и SEF
параллельна прямой SF
, так как параллельны плоскости \alpha
и SBC
. Тогда, если прямая n
пересекается с прямыми SE
и EF
в точках Q
и K
соответственно, то треугольник EQK
— равнобедренный, так как он подобен равнобедренному треугольнику SEF
. Обозначим \angle QKE=\angle SFH=\beta
. Тогда
\tg\beta=\frac{SH}{HF}=\sqrt{14},~\cos\beta=\frac{1}{\sqrt{1+\tg^{2}\beta}}=\frac{1}{\sqrt{15}},
KH=EH-EK=EH-AA_{2}=1-\frac{4}{5}=\frac{1}{5}.
Пусть OG
— перпендикуляр, опущенный из центра окружности на QK
. Тогда длина отрезка OG
равна искомому расстоянию от центра сферы до плоскости \alpha
. Пусть прямые SH
и QK
пересекаются в точке T
. Из прямоугольного треугольника KHT
находим, что
HT=KH\tg\angle HKT=\frac{1}{5}\tg\beta=\frac{1}{5}\sqrt{14}.
Следовательно,
OG=OT\cos\angle TOG=(SH-SO+HT)\cos\beta=(SH-R+HT)\cos\beta=
=\left(\sqrt{14}-\frac{8}{\sqrt{14}}+\frac{1}{5}\sqrt{14}\right)\frac{1}{\sqrt{15}}=\left(\sqrt{14}-\frac{4\sqrt{14}}{7}+\frac{\sqrt{14}}{5}\right)\frac{1}{\sqrt{15}}=
=\left(\frac{3\sqrt{14}}{7}+\frac{\sqrt{14}}{5}\right)\frac{1}{\sqrt{15}}=\frac{22\sqrt{14}}{35\sqrt{15}}.
Источник: Вступительный экзамен в МФТИ. — 2002, билет 1, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 02-1-6, с. 405


