8703. Расстояние от центра O
шара радиуса 12, описанного около правильной четырёхугольной пирамиды, до бокового ребра равно 4\sqrt{2}
. Найдите:
1) высоту пирамиды;
2) расстояние от точки O
до боковой грани пирамиды;
3) радиус вписанного в пирамиду шара.
Ответ. \frac{56}{3}
; 3\sqrt{2}
; \frac{8}{3}(2\sqrt{2}-1)
.
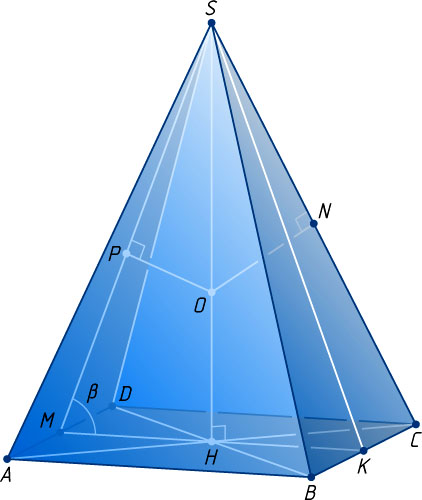
Решение. 1) Пусть ON
— перпендикуляр, опущенный из центра O
описанной сферы на боковое ребро SC
правильной четырёхугольной пирамиды SABCD
с вершиной S
(рис. 1), SH
— высота пирамиды. Поскольку SO
— радиус описанной сферы, из прямоугольного треугольника SON
находим, что
SN=\sqrt{SO^{2}-ON^{2}}=\sqrt{144-16\cdot2}=4\sqrt{9-2}=4\sqrt{7}.
Перпендикуляр, опущенный из центра сферы на хорду, делит её пополам, поэтому SC=2SN=8\sqrt{7}
. Прямоугольные треугольники SHC
и SNO
подобны, значит, \frac{SH}{SN}=\frac{SC}{SO}
, откуда
SH=SN\cdot\frac{SC}{SO}=4\sqrt{7}\cdot\frac{8\sqrt{7}}{12}=\frac{56}{3}.
2) Обозначим AB=BC=CD=AD=a
. Тогда CH=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}
. Из прямоугольного треугольника SHC
получаем, что CH=\frac{16\sqrt{2}}{3}
. Из уравнения \frac{a\sqrt{2}}{2}=\frac{16\sqrt{2}}{3}
находим, что a=\frac{16\sqrt{7}}{3}
.
Пусть OP
— перпендикуляр, опущенный из точки O
на медиану SM
равнобедренного треугольника ASD
. Так как прямая AD
перпендикулярна пересекающимся прямым AD
и SH
плоскости SHM
, то AD\perp OP
, значит, OP
— перпендикуляр к плоскости боковой грани ASD
. В прямоугольном треугольнике SHM
известно, что
SH=\frac{56}{3},~HM=\frac{a}{2}=\frac{8\sqrt{7}}{3},~SO=12.
Тогда
SM=\sqrt{SH^{2}+HM^{2}}=\sqrt{\left(\frac{56}{3}\right)^{2}+\left(\frac{8\sqrt{7}}{3}\right)^{2}}=\frac{16\sqrt{14}}{3}.
Из подобия прямоугольных треугольников SPO
и SHM
находим, что
OP=MH\cdot\frac{SO}{SM}=\frac{8\sqrt{7}}{3}\cdot\frac{12}{\frac{16\sqrt{14}}{3}}=3\sqrt{2}.
3) Пусть \beta
— угол между боковой гранью пирамиды SABCD
и плоскостью её основания. Поскольку пирамида правильная, центр Q
её вписанного шара лежит на высоте SH
, шар касается плоскости основания в точке H
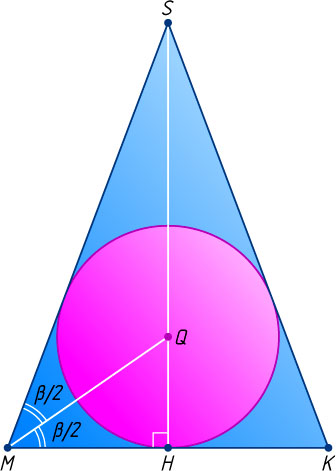
, а плоскостей боковых граней — в точках, лежащих на апофемах пирамиды. Проведём сечение через апофему SM
и апофему SK
, лежащую в грани BSC
(рис. 2). Получим равнобедренный треугольник MSK
и вписанную в него окружность с центром Q
радиуса r
, равного радиусу сферы, вписанной в пирамиду. Поскольку SMH
— линейный угол двугранного угла между плоскостью боковой грани пирамиды и плоскостью её основания, \angle SMH=\beta
.
Из прямоугольного треугольника SMH
находим, что
\tg\beta=\frac{SH}{HM}=\frac{\frac{56}{3}}{\frac{8\sqrt{7}}{3}}=\sqrt{7}.
Применив формулу \tg\beta=\frac{2\tg\frac{\beta}{2}}{1-\tg^{2}\frac{\beta}{2}}
, получим уравнение
\sqrt{7}=\frac{2\tg\frac{\beta}{2}}{1-\tg^{2}\frac{\beta}{2}},
из которого находим, что \tg\frac{\beta}{2}=\frac{2\sqrt{2}-1}{\sqrt{7}}
, а так как MQ
— биссектриса угла SMH
, то из прямоугольного треугольника QHM
находим, что
r=QH=MH\tg\frac{\beta}{2}=\frac{8\sqrt{7}}{3}\cdot\frac{2\sqrt{2}-1}{\sqrt{7}}=\frac{8}{3}(2\sqrt{2}-1).
Источник: Вступительный экзамен в МФТИ. — 2002, билет 5, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 02-5-6, с. 408

