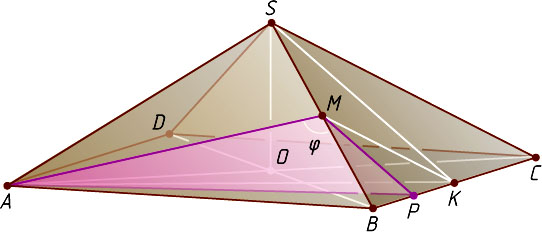
8707. Сторона основания ABCD
правильной пирамиды SABCD
равна 8, высота SO
равна 3. Точка M
— середина ребра SB
, точка K
— середина ребра BC
. Найдите:
1) объём пирамиды AMSK
;
2) угол между прямыми AM
и SK
;
3) расстояние между прямыми AM
и SK
.
Ответ. 8; \arccos\frac{3}{5}
; \frac{24}{13}
.
Решение. 1) Пусть V
— объём пирамиды SABCD
. Тогда
V=\frac{1}{3}S_{ABCD}\cdot SO=\frac{1}{3}\cdot64\cdot3=64,~V_{SABC}=\frac{1}{2}V=32.
Рассмотрим треугольную пирамиду SABC
с вершиной B
. Плоскость AMK
отсекает от неё треугольную пирамиду AMSK
с вершиной B
, поэтому
V_{AMSK}=\frac{BM}{BS}\cdot\frac{BK}{BC}\cdot\frac{BA}{BA}\cdot V_{SABC}=\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{1}\cdot32=\frac{1}{4}\cdot32=8.
2) Пусть P
— середина отрезка BK
. Тогда MP
— средняя линия треугольника BKS
, поэтому
MP=\frac{1}{2}SK=\frac{1}{2}\sqrt{SO^{2}-OK^{2}}=\frac{1}{2}\sqrt{9+16}=\frac{5}{2},
а так как MP\parallel SK
, то угол между прямыми AM
и SK
равен углу между прямыми AM
и MP
.
Из прямоугольных треугольников ABP
и SKB
находим, что
AP^{2}=AB^{2}+BP^{2}=64+4=68,~BS^{2}=SK^{2}+BK^{2}=25+16=41.
По формуле для медианы из равнобедренного треугольника ASB
находим, что
AM=\frac{1}{2}\sqrt{2AS^{2}+2AB^{2}-BS^{2}}=\frac{1}{2}\sqrt{2\cdot41+2\cdot64-41}=\frac{13}{2}.
Обозначим \angle AMP=\varphi
. По теореме косинусов
\cos\varphi=\cos\angle AMP=\frac{AM^{2}+MP^{2}-AP^{2}}{2AM\cdot MP}=\frac{\frac{169}{4}+\frac{25}{4}-68}{2\cdot\frac{13}{2}\cdot\frac{5}{2}}=\frac{3}{5}.
3) Воспользуемся формулой V=\frac{1}{6}abc\sin\varphi
, где V
— объём тетраэдра, a
и b
— длины двух его противоположных рёбер, c
расстояние между этими рёбрами, \varphi
— угол между ними. В нашем случае
V_{AMSK}=\frac{1}{6}AM\cdot SK\cdot c\cdot\sin\varphi,
где c
— искомое расстояние между прямыми AM
и SK
. Из уравнения
8=\frac{1}{6}\cdot\frac{13}{2}\cdot5\cdot c\cdot\frac{4}{5}
находим, что c=\frac{24}{13}
.
Источник: Вступительный экзамен в МФТИ. — 2002, билет 9, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 02-9-4, с. 411