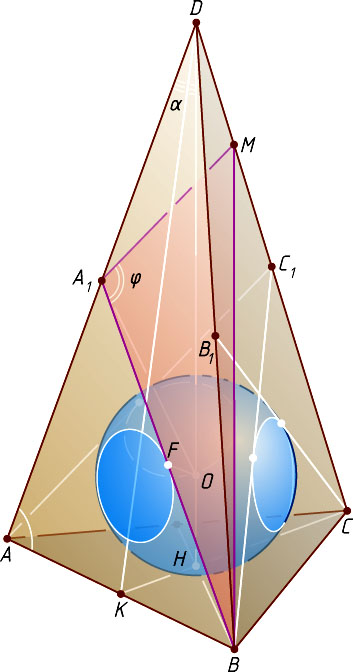
8711. Сторона основания ABC
правильной пирамиды ABCD
равна 4\sqrt{3}
, \angle DAB=\arctg\sqrt{\frac{37}{3}}
Точки A_{1}
, B_{1}
, C_{1}
— середины рёбер AD
, BD
, CD
соответственно. Найдите:
1) угол между прямыми BA_{1}
и AC_{1}
;
2) расстояние между прямыми BA_{1}
и AC_{1}
;
3) радиус сферы, касающейся плоскости ABC
и отрезков AC_{1}
, BA_{1}
и CB_{1}
.
Ответ. \arccos\frac{11}{32}
; \frac{36}{\sqrt{301}}
; 2.
Решение. 1) Пусть K
— середина AB
. Из прямоугольного треугольника ADK
находим, что
AD=\frac{AK}{\cos\angle DAB}=AK\sqrt{1+\tg^{2}\angle DAB}=2\sqrt{3}\cdot\sqrt{1+\frac{37}{3}}=4\sqrt{10}.
По формуле для медианы треугольника
BA_{1}^{2}=\frac{1}{4}(2BD^{2}+2AB^{2}-AD^{2})=\frac{1}{4}(2\cdot160+2\cdot48-160)=64,
значит, BC_{1}=AC_{1}=BA_{1}=8
.
Пусть M
— середина отрезка DC_{1}
. Тогда A_{1}M
— средняя линия треугольника ADC_{1}
, значит, A_{1}M=\frac{1}{2}AC_{1}=4
, а так как A_{1}M\parallel AC_{1}
, то угол между скрещивающимися прямыми BA_{1}
и AC_{1}
равен углу между пересекающимися прямыми BA_{1}
и A_{1}M
.
Из треугольника DBC_{1}
по формуле для медианы находим, что
BM^{2}=\frac{1}{4}(2BC_{1}^{2}+2BD^{2}-DC_{1}^{2})=\frac{1}{4}(2\cdot64+2\cdot160-40)=102.
По теореме косинусов
\cos\angle BA_{1}M=\frac{A_{1}M^{2}+BA_{1}^{2}-BM^{2}}{2A_{1}M\cdot BA_{1}}=\frac{16+64-102}{2\cdot4\cdot8}=-\frac{11}{32}.
Пусть \varphi
— искомый угол. Угол между прямыми не может быть больше 90^{\circ}
, поэтому
\cos\varphi=\cos(180^{\circ}-\angle BA_{1}M)=-\cos\angle BA_{1}M=\frac{11}{32},
\sin\varphi=\sqrt{1-\cos^{2}\varphi}=\sqrt{1-\left(\frac{11}{32}\right)^{2}}=\frac{\sqrt{3}\cdot\sqrt{301}}{32}.
2) Пусть DH
— высота пирамиды ABCD
, V
— её объём. Тогда
AH=\frac{2}{3}\cdot\frac{BC\sqrt{3}}{2}=\frac{2}{3}\cdot\frac{4\sqrt{3}\cdot\sqrt{3}}{2}=4,~DH=\sqrt{AD^{2}-AH^{2}}=\sqrt{160-16}=12.
V=\frac{1}{3}S_{\triangle ABC}\cdot DH=\frac{1}{3}\cdot\frac{(4\sqrt{3})^{2}\sqrt{3}}{4}\cdot12=48\sqrt{3}.
Рассмотрим тетраэдр ABCD
с вершиной C
и тетраэдр AC_{1}BA_{1}
с вершиной C_{1}
. Высота тетраэдра AC_{1}BA_{1}
, проведённая из вершины C_{1}
, вдвое меньше высоты тетраэдра ABCD
, проведённой из вершины C
, а S_{\triangle ABA_{1}}=\frac{1}{2}S_{\triangle ABD}
, поэтому
V_{AC_{1}BA_{1}}=\frac{1}{2}\cdot\frac{1}{2}V_{ABCD}=\frac{1}{4}V=12\sqrt{3}.
С другой стороны,
V_{AC_{1}BA_{1}}=\frac{1}{6}BA_{1}\cdot AC_{1}\cdot d\cdot\sin\varphi,
где d
— искомое расстояние между прямыми BA_{1}
и AC_{1}
. Из уравнения
12\sqrt{3}=\frac{1}{6}\cdot8\cdot8\cdot d\cdot\frac{\sqrt{3}\cdot\sqrt{301}}{32}
находим, что d=\frac{36}{\sqrt{301}}
.
3) Можно доказать, что центр O
указанной сферы радиуса r
лежит на высоте DH
пирамиды и сфера касается плоскости основания в точке H
. Если F
— точка касания сферы с прямой BA_{1}
, то BH=BF
как отрезки касательных, проведённых к сфере из одной точки, а так как BH=AH=4
, а BA_{1}=8
, то BF=\frac{1}{2}BA_{1}
, т. е. F
— середина BA_{1}
.
Обозначим \angle ADH=\alpha
. Из прямоугольных треугольников ADH
и A_{1}OF
находим, что
\cos\alpha=\frac{DH}{AD}=\frac{12}{4\sqrt{10}}=\frac{3}{\sqrt{10}},
OA_{1}^{2}=OF^{2}+A_{1}F^{2}=r^{2}+16,
а так как DO=DH-OH=12-r
, то применяя теорему косинусов к треугольнику ODA_{1}
, получим уравнение
r^{2}+16=4\cdot10+(12-r)^{2}-2\cdot2\sqrt{10}\cdot(12-r)\cdot\frac{3}{\sqrt{10}},
из которого находим, что r=2
.
Источник: Вступительный экзамен в МФТИ. — 2001, билет 1, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 01-1-6, с. 395
