8715. Три шара радиуса r
касаются друг друга и шара радиуса R
внешним образом. При каком соотношении между r
и R
это возможно? Считая, что R\gt r
, найдите радиус шара, касающегося всех четырёх шаров внешним образом.
Ответ. R\geqslant\left(\frac{2}{\sqrt{3}}-1\right)r
; \frac{R\left(R+r-\sqrt{R^{2}+2Rr-\frac{r^{2}}{3}}\right)}{r+\sqrt{R^{2}+2Rr-\frac{r^{2}}{3}}-R}
.
Решение. Пусть A
, B
и C
— центры шаров радиуса r
, D
— центр шара радиуса R
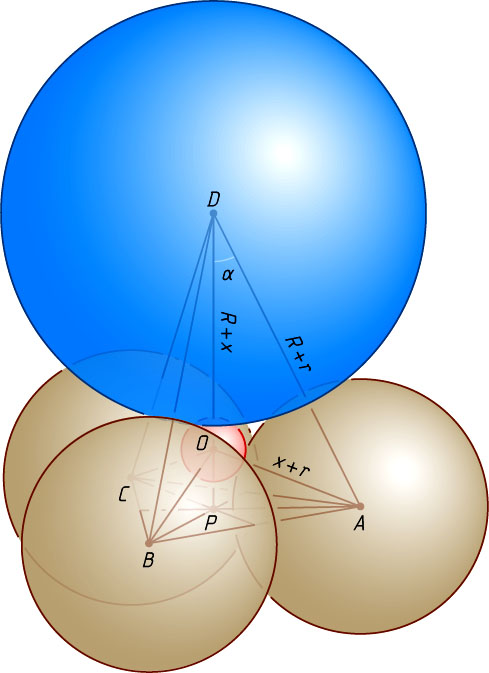
. Поскольку линия центров двух касающихся шаров проходит через их точку касания, рёбра пирамиды ABCD
равны DA=DB=DC=r+R
, AB=BC=AC=2r
, значит, ABCD
— правильная пирамида с вершиной D
.
Пусть O
— центр шара радиуса x
, касающегося четырёх данных шаров. Тогда OA=OB=OC=r+x
и OD=R+x
. Точка O
равноудалена от вершин равностороннего треугольника ABC
, значит, она лежит на прямой DP
, где P
— центр равностороннего треугольника ABC
. Чтобы шар радиуса R
касался трёх шаров радиуса r
должно выполняться условие AD\gt AP
, т. е. r+R\geqslant\frac{2r\sqrt{3}}{3}
, откуда R\geqslant\left(\frac{2}{\sqrt{3}}-1\right)r
.
Обозначим \angle ADP=\angle BDP=\angle CDP=\alpha
. Из прямоугольного треугольника ADP
находим, что
\sin\alpha=\frac{AP}{AD}=\frac{\frac{2r\sqrt{3}}{3}}{r+R}.
Тогда
\cos\alpha=\sqrt{1-\sin^{2}\alpha}=\sqrt{1-\left(\frac{\frac{2r\sqrt{3}}{3}}{r+R}\right)^{2}}=\frac{\sqrt{R^{2}+2Rr-\frac{r^{2}}{3}}}{r+R}.
Из треугольника ADO
по теореме косинусов находим, что
AO^{2}=AD^{2}+DO^{2}-2AD\cdot DO\cos\alpha,
или
(x+r)^{2}=(r+R)^{2}+(x+R)^{2}-2(r+R)(x+R)\cdot\frac{\sqrt{R^{2}+2Rr-\frac{r^{2}}{3}}}{r+R},
откуда
x=\frac{R\left(R+r-\sqrt{R^{2}+2Rr-\frac{r^{2}}{3}}\right)}{r+\sqrt{R^{2}+2Rr-\frac{r^{2}}{3}}-R}.
Подкоренное выражение неотрицательно, так как из неравенства r+R\geqslant\frac{2r\sqrt{3}}{3}
следует неравенство R^{2}+2Rr-\frac{r^{2}}{3}\geqslant0
.
Источник: Вступительный экзамен в МФТИ. — 2001, билет 5, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 01-5-6, с. 398
