8719. Апофема правильной пирамиды SABCD
равна 2, боковое ребро образует с основанием ABCD
угол, равный \arctg\sqrt{\frac{3}{2}}
. Точки E
, F
, K
выбраны соответственно на рёбрах AB
, AD
, SC
так, что \frac{AE}{EB}=\frac{AF}{FD}=\frac{SK}{KC}=\frac{1}{2}
. Найдите:
1) площадь сечения пирамиды плоскостью EFK
;
2) расстояние от точки D
до плоскости EFK
;
3) угол между прямой SD
и плоскостью EFK
.
Ответ. \frac{14}{9}\sqrt{\frac{5}{3}}
; \frac{4}{3\sqrt{5}}
; \arcsin\frac{3}{5}
.
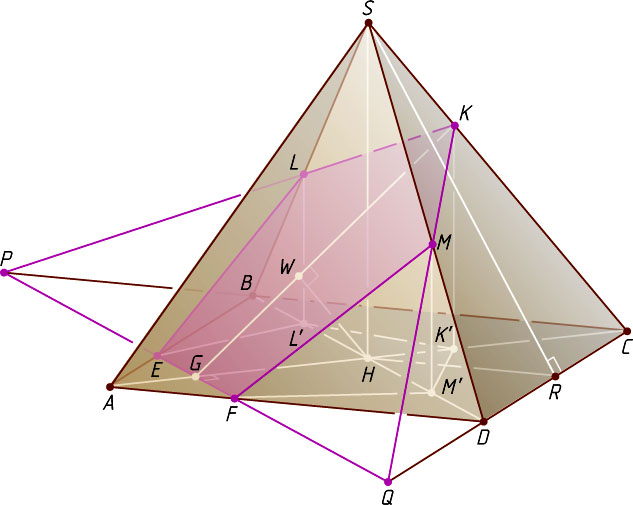
Решение. 1) Пусть прямая EF
пересекает продолжения рёбер BC
и CD
в точках P
и Q
соответственно, прямая KP
пересекает ребро SB
в точке L
, а прямая KQ
пересекает ребро SD
в точке M
(рис. 1). Тогда пятиугольник EFMKL
— сечение о котором говорится в условии задачи.
Обозначим через a
сторону квадрата ABCD
. Поскольку AE=AF=\frac{a}{3}
, треугольник EAF
— равнобедренный и прямоугольный. Тогда DQ=DF=\frac{2}{3}a
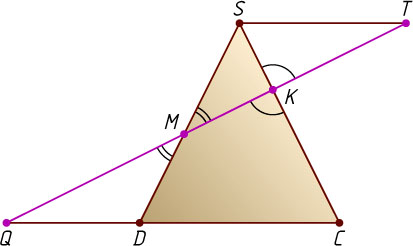
. Через вершину S
проведём прямую, параллельную CD
, и продолжим QK
до пересечения с этой прямой в точке T
(рис. 2). Из подобия треугольников SKT
и CKQ
следует, что
ST=CQ\cdot\frac{SK}{KC}=(CD+DQ)\cdot\frac{1}{2}=\frac{1}{2}\left(a+\frac{2}{3}a\right)=\frac{5}{6}a,
а из подобия треугольников SMT
и DMQ
—
\frac{SM}{MD}=\frac{ST}{DQ}=\frac{\frac{5}{6}a}{\frac{2}{3}a}=\frac{5}{4}.
Аналогично докажем, что \frac{SL}{LB}=\frac{5}{4}
.
Пусть H
, M'
, K'
, L'
— ортогональные проекции точек соответственно S
, M
, K
и L
на плоскость основания пирамиды. Точки M'
, K'
и L'
лежат на отрезках DH
, CH
и BH
, причём
\frac{HM'}{M'D}=\frac{SM}{MD}=\frac{5}{4},~\frac{HK'}{K'C}=\frac{SK}{KC}=\frac{1}{2},~\frac{HL'}{L'B}=\frac{SL}{LB}=\frac{5}{4},
а SH
— высота пирамиды SABCD
.
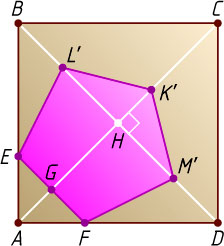
Найдём площадь пятиугольника EFM'K'L'
— ортогональной проекции нашего сечения на плоскость основания пирамиды (рис. 3). Этот пятиугольник состоит из равнобедренной трапеции EFM'L'
с основаниями
EF=\frac{1}{3}BD=\frac{a\sqrt{2}}{3},~M'L'=\frac{5}{9}BD=\frac{5a\sqrt{2}}{9},
высотой GH=\frac{1}{3}AC=\frac{a\sqrt{2}}{3}
и равнобедренного треугольника M'K'L'
с основанием L'M'=\frac{5a\sqrt{2}}{9}
и высотой K'H=\frac{1}{6}AC=\frac{a\sqrt{2}}{6}
. Поэтому
S_{EFM'K'L'}=S_{EFM'L'}+S_{\triangle M'K'L'}=\frac{1}{2}(EF+M'L')\cdot GH+\frac{1}{2}M'L'\cdot K'H=
=\frac{1}{2}\left(\frac{a\sqrt{2}}{3}+\frac{5a\sqrt{2}}{9}\right)\cdot\frac{a\sqrt{2}}{3}+\frac{1}{2}\cdot\frac{5a\sqrt{2}}{9}\cdot\frac{a\sqrt{2}}{6}=\frac{7}{18}a^{2}.
Пусть R
— середина CD
. Из прямоугольных треугольников SHC
и SHR
находим, что
SH=CH\tg\angle SCH=\frac{a\sqrt{2}}{2}\cdot\sqrt{\frac{3}{2}}=\frac{a\sqrt{3}}{2},
4=SR^{2}=SH^{2}+HR^{2}=\frac{3}{4}a^{2}+\frac{1}{4}a^{2}=a^{2},
откуда a=2
. Тогда
S_{EFM'K'L'}=\frac{7}{18}a^{2}=\frac{14}{9},~SH=\frac{a\sqrt{3}}{2}=\sqrt{3},~K'G=\frac{a\sqrt{2}}{2}=\sqrt{2}.
Из подобия треугольников KK'C
и SHC
находим, что
KK'=SH\cdot\frac{CK}{SC}=\sqrt{3}\cdot\frac{2}{3}=\frac{2\sqrt{3}}{3}.
Так как CG\perp PQ
и KG\perp PQ
, то KGK'
— линейный угол двугранного угла между плоскостями сечения и основания пирамиды. Обозначим \angle KGK'=\varphi
. Тогда
\tg\varphi=\frac{KK'}{K'G}=\frac{\frac{2\sqrt{3}}{3}}{\sqrt{2}}=\sqrt{\frac{2}{3}},~\cos\varphi=\frac{1}{\sqrt{1+\tg^{2}\varphi}}=\frac{1}{\sqrt{1+\frac{2}{3}}}=\sqrt{\frac{3}{5}}.
Следовательно,
S_{EFMKL}=\frac{S_{EFM'K'L'}}{\cos\varphi}=\frac{\frac{14}{9}}{\sqrt{\frac{3}{5}}}=\frac{14}{9}\sqrt{\frac{5}{3}}.
2) Прямая BD
параллельна прямой EF
, лежащей в секущей плоскости, значит, прямая BD
параллельна секущей плоскости, поэтому все её точки равноудалены от этой плоскости. Из точки H
, лежащей на прямой BD
, опустим перпендикуляр HW
на прямую GK
. Тогда HW
— перпендикуляр к плоскости EFK
. Из прямоугольного треугольника GWH
находим, что
HW=GH\cdot\sin\varphi=\frac{a\sqrt{2}}{3}\cdot\tg\varphi\cos\varphi=\frac{2\sqrt{2}}{3}\cdot\sqrt{\frac{2}{3}}\cdot\sqrt{\frac{3}{5}}=\frac{4}{3\sqrt{5}}.
Следовательно, расстояние от точки D
до плоскости EKF
также равно \frac{4}{3\sqrt{5}}
.
3) Из прямоугольного треугольника SRD
находим, что
SD=\sqrt{SR^{2}+DR^{2}}=\sqrt{4+1}=\sqrt{5}.
Тогда DM=\frac{4}{9}SD=\frac{4\sqrt{5}}{9}
. Синус угла между наклонной DM
и плоскостью сечения равен отношению расстояния от точки D
до этой плоскости к длине наклонной DM
, т. е.
\frac{HW}{DM}=\frac{\frac{4}{3\sqrt{5}}}{\frac{4\sqrt{5}}{9}}=\frac{3}{5}.
Источник: Вступительный экзамен в МФТИ. — 2001, билет 9, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 01-9-4, с. 401


