8723. Сфера касается боковых граней четырёхугольной пирамиды SABCD
в точках, лежащих на рёбрах AB
, BC
, CD
, DA
. Известно, что высота пирамиды равна 2\sqrt{5}
, AB=6
, SA=5
, SB=7
, SC=2\sqrt{10}
. Найдите длины рёбер BC
и CD
, радиус сферы и двугранный угол при ребре SD
.
Ответ. BC=9
, CD=\frac{24}{5}
; R=2\sqrt{\frac{6}{5}}
; \varphi=2\arcsin\sqrt{\frac{77}{87}}
.
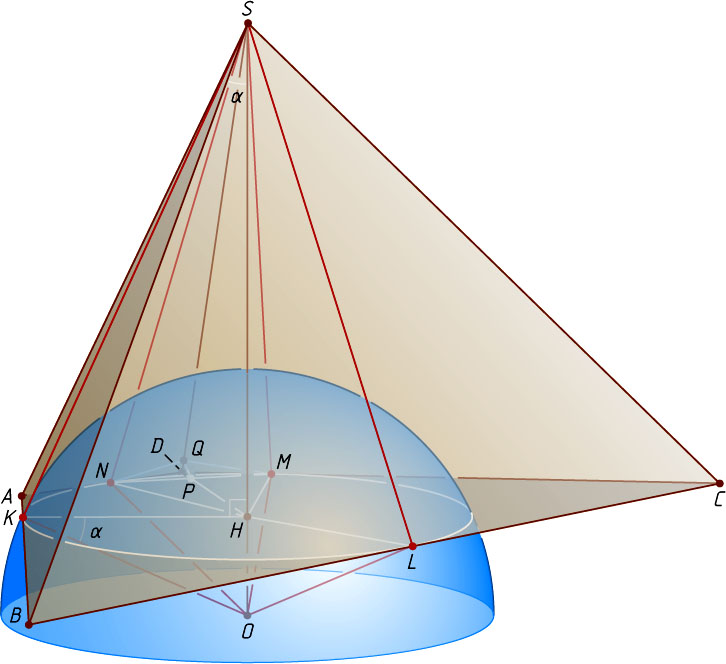
Решение. Пусть K
, L
, M
и N
— точки касания сферы с боковыми гранями ASB
, BSC
, CSD
и ASD
соответственно (рис. 1), SH
— высота пирамиды, O
— центр сферы, R
— её радиус, H_{1}
— точка касания сферы с плоскостью основания пирамиды.
Радиус OK
, проведённый в точку касания сферы с плоскостью ASB
, перпендикулярен этой плоскости, поэтому OK\perp SK
, значит, треугольник SKO
— прямоугольный. Аналогично, треугольники SLO
, SMO
и SNO
— также прямоугольные, причём все они равны по катету и гипотенузе. Следовательно, SN=SM=SL=SK
. Тогда боковые рёбра четырёхугольной пирамиды SKLMN
равны между собой, значит, её высота SH
проходит через центр окружности, описанной около четырёхугольника KLMN
, т. е. через центр окружности, по которой сфера пересекается с основанием пирамиды SABCD
(или, что то же самое, окружности, вписанной в четырёхугольник ABCD
). Аналогично докажем, что высота OH_{1}
четырёхугольной пирамиды OKLMN
также проходит через центр этой окружности, поэтому точки H
и H_{1}
совпадают, а прямая SO
проходит через центр H
окружности, вписанной в четырёхугольник ABCD
.
Отрезок HK
— радиус окружности, проведённый в точку касания с прямой AB
, поэтому HK\perp AB
. Тогда по теореме о трёх перпендикулярах SK\perp AB
, т. е. SK
— высота треугольника ASB
. По формуле Герона
S_{\triangle ASB}=\sqrt{9(9-5)(9-6)(9-7)}=\sqrt{9\cdot4\cdot3\cdot2}=6\sqrt{6}.
С другой стороны,
S_{\triangle ASB}=\frac{1}{2}AB\cdot SK=\frac{1}{2}\cdot6\cdot SK=3SK,
Из уравнения 3SK=6\sqrt{6}
находим, что SK=2\sqrt{6}
. Тогда SN=SM=SL=SK=2\sqrt{6}
.
Из прямоугольного треугольника SHK
находим, что
HK=\sqrt{SK^{2}-SH^{2}}=\sqrt{(2\sqrt{6})^{2}-(2\sqrt{5})^{2}}=\sqrt{24-20}=2.
Тогда HN=HM=HL=HK=2
.
В прямоугольном треугольнике SKO
отрезок HK
— высота, проведённая из вершины прямого угла. Обозначим \angle OSK=\angle HKO=\alpha
. Тогда
\cos\alpha=\frac{SH}{SK}=\frac{2\sqrt{5}}{2\sqrt{6}}=\sqrt{\frac{5}{6}}.
Следовательно,
R=OK=\frac{HK}{\cos\alpha}=\frac{2}{\sqrt{\frac{5}{6}}}=2\sqrt{\frac{6}{5}}.
Из прямоугольных треугольников SKB
и SLC
находим, что
BK=\sqrt{SB^{2}-SK^{2}}=\sqrt{7^{2}-(2\sqrt{6})^{2}}=\sqrt{49-24}=5,
LC=\sqrt{SC^{2}-SL^{2}}=\sqrt{(2\sqrt{10})^{2}-(2\sqrt{6})^{2}}=\sqrt{40-24}=4,
поэтому
BL=BK=5,~CM=CL=4,~BC=BL+CL=5+4=9,~AN=AK=AB-BK=6-5=1.
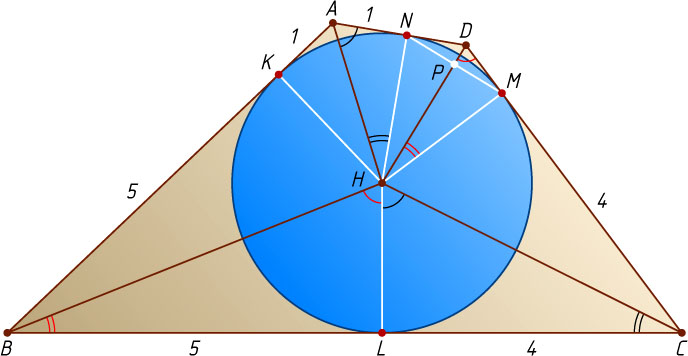
Прямоугольные треугольники LHC
и NAH
подобны (рис. 2), так как их катеты соответственно пропорциональны (\frac{HL}{LC}=\frac{AN}{NH}=\frac{1}{2}
), поэтому
\angle AHN+\angle CHL=\angle AHN+\angle NAH=90^{\circ},
\angle KHN+\angle MHL=2\angle AHN+2\angle CHL=2(\angle AHN+\angle CHL)=2\cdot90^{\circ}=180^{\circ},
\angle KHL+\angle MHN=360^{\circ}-\angle KHN+\angle MHL=360^{\circ}-180^{\circ}=180^{\circ},
\angle BHL+\angle DHM=\frac{1}{2}(\angle KHL+\angle MHN)=90^{\circ}.
Следовательно, прямоугольные треугольники DMH
и HLB
подобны по двум углам, значит, \frac{DM}{HL}=\frac{HM}{BL}
, откуда
DM=HL\cdot\frac{HM}{BL}=2\cdot\frac{2}{5}=\frac{4}{5},~CD=CM+DM=4+\frac{4}{5}=\frac{24}{5}.
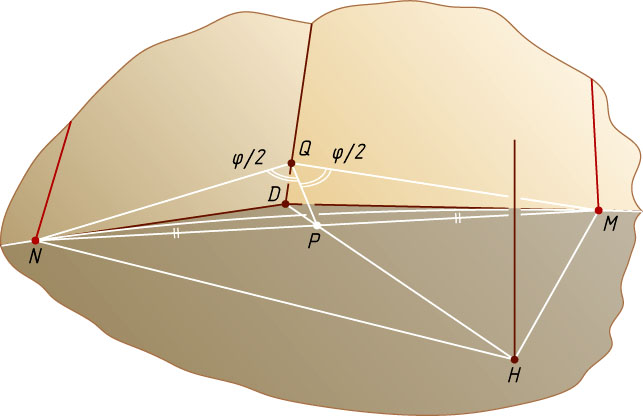
Рассмотрим четырёхугольник MDNH
. Пусть его диагонали DH
и MN
пересекаются в точке P
. Поскольку DM=DN
и HM=HN
, DH
— серединный перпендикуляр к отрезку MN
, поэтому P
— середина MN
и MN\perp DH
. Обозначим \angle MDH=\beta
. Из прямоугольного треугольника MDH
находим, что
\ctg\beta=\frac{DM}{MH}=\frac{\frac{4}{5}}{2}=\frac{2}{5},~\sin\beta=\frac{1}{\sqrt{1+\ctg^{2}\beta}}=\frac{1}{\sqrt{1+\frac{4}{25}}}=\frac{5}{\sqrt{29}}.
Тогда
PM=DM\sin\beta=\frac{4}{5}\cdot\frac{5}{\sqrt{29}}=\frac{4}{\sqrt{29}}.
По теореме о трёх перпендикулярах MN\perp SD
. Из точки P
опустим перпендикуляр PQ
на ребро SD
. Тогда плоскость MQN
перпендикулярна прямой SD
, поскольку прямая SD
перпендикулярна двум пересекающимся прямым MN
и PQ
этой плоскости, поэтому MQN
— линейный угол двугранного угла между плоскостями боковых граней ASD
и CSD
. Обозначим \angle MQN=\varphi
. Из прямоугольного треугольника DMS
в котором MQ
— высота, проведённая из вершины прямого угла, находим, что
MQ=\frac{DM\cdot MS}{SD}=\frac{\frac{4}{5}\cdot2\sqrt{6}}{\sqrt{\frac{16}{25}+24}}=\frac{4\sqrt{3}}{\sqrt{77}}.
Следовательно,
\sin\frac{\varphi}{2}=\sin\angle PQM=\frac{PM}{MQ}=\frac{\frac{4}{\sqrt{29}}}{\frac{4\sqrt{3}}{\sqrt{77}}}=\sqrt{\frac{77}{87}}.
Источник: Вступительный экзамен в МФТИ. — 2005, билет 5, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 05-5-6, с. 440


