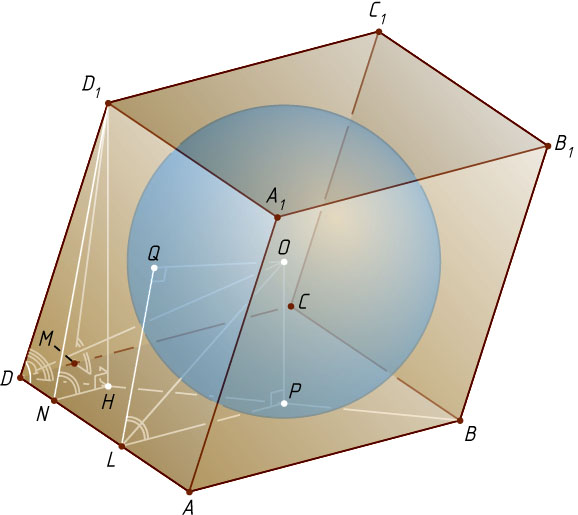
8731. В основании призмы ABCDA_{1}B_{1}C_{1}D_{1}
лежит прямоугольник ABCD
. Острые углы D_{1}DA
и D_{1}DC
равны между собой, угол между ребром DD_{1}
и плоскостью основания призмы равен \arccos\frac{1}{\sqrt{13}}
, а CD=5\sqrt{6}
. Все грани призмы касаются некоторой сферы. Найдите BC
и угол между плоскостями D_{1}DC
и ABC
, а также расстояние от точки D
до центра сферы.
Ответ. 5\sqrt{6}
, \arccos\frac{1}{5}
, 12.
Решение. Поскольку в призму можно вписать сферу, все высоты призмы равны диаметру сферы как расстояния между противоположными гранями, а так как площадь грани призмы равна объёму призмы, делённому на высоту, то все грани призмы равновелики. В частности, S_{ADD_{1}A_{1}}=S_{CDD_{1}C_{1}}
, или AD\cdot DD_{1}\sin\angle D_{1}DA=CD\cdot DD_{1}\sin\angle D_{1}DC
, откуда AD=CD=5\sqrt{6}
. Следовательно, BC=AD=5\sqrt{6}
, т. е. ABCD
— квадрат.
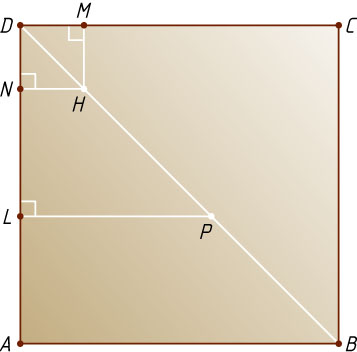
Пусть D_{1}M
и D_{1}N
— высоты параллелограммов DD_{1}C_{1}C
и DD_{1}A_{1}A
, опущенные из вершины D_{1}
(рис. 1). Из равенства площадей граней DD_{1}C_{1}C
, DD_{1}A_{1}A
и ABCD
следует, что D_{1}M=D_{1}N=AD=5\sqrt{6}
.
Пусть H
— основание перпендикуляра, опущенного из вершины D_{1}
на плоскость грани ABCD
. По теореме о трёх перпендикулярах HM\perp DC
и HN\perp AD
, поэтому D_{1}MH
и D_{1}NH
— линейные углы двугранных углов при рёбрах DC
и AD
параллелепипеда. Прямоугольные треугольники D_{1}HM
и D_{1}HN
равны по катету и гипотенузе, значит, HM=HN
, т. е. точка H
равноудалена от сторон прямого угла ADC
, поэтому луч DH
— биссектриса этого угла (рис. 2). Обозначим, D_{1}D=x
. Из прямоугольных треугольников D_{1}HD
, DMH
, D_{1}MD
и D_{1}HM
находим, что
DH=DD_{1}\cos\angle D_{1}DH=x\cdot\frac{1}{\sqrt{13}}=\frac{x}{\sqrt{13}},
DM=MH=\frac{DH}{\sqrt{2}}=\frac{x}{\sqrt{2}\cdot\sqrt{13}},
\sqrt{D_{1}D^{2}-DM^{2}}=D_{1}M,~\mbox{или}~\sqrt{x^{2}-\frac{x^{2}}{26}}=5\sqrt{6},
откуда x=2\sqrt{3}\cdot\sqrt{13}
. Тогда DM=\frac{DH}{\sqrt{2}}=\sqrt{6}
, а если \varphi
— искомый угол между плоскостями D_{1}DC
и ABC
, то
\cos\varphi=\cos\angle D_{1}NH=\cos\angle D_{1}MH=\frac{MH}{D_{1}M}=\frac{\sqrt{6}}{5\sqrt{6}}=\frac{1}{5}.
Пусть O
— центр вписанной сферы радиуса r
, P
и Q
— точки касания с плоскостями граней ABCD
и D_{1}DAA_{1}
. Прямая AD
перпендикулярна плоскости, проходящей через пересекающиеся прямые OP
и OQ
, так как она перпендикулярна прямым OP
и OQ
, значит, если L
точка пересечения этой плоскости с прямой AD
, то PLQ
— также двугранный угол между плоскостями граней ABCD
и D_{1}DAA_{1}
т. е. \angle PLQ=\varphi
.
Заметим, что точка P
равноудалена от сторон угла ADC
, поэтому она лежит на биссектрисе этого угла, т. е. на луче DH
. Рассмотрим сечение параллелепипеда плоскостью PLQ
. Поскольку O
— центр окружности, вписанной в угол PLQ
, луч LO
— биссектриса угла PLQ
. Подставив \cos\varphi=\frac{1}{5}
в правую часть формулы \cos\varphi=\frac{1-\tg^{2}\frac{\varphi}{2}}{1+\tg^{2}\frac{\varphi}{2}}
, получим, что \tg\frac{\varphi}{2}=\sqrt{\frac{2}{3}}
. Тогда
PL=\frac{OP}{\tg\frac{\varphi}{2}}=\frac{r}{\tg\frac{\varphi}{2}}=\frac{6}{\sqrt{\frac{2}{3}}}=3\sqrt{6},
DP=PL\sqrt{2}=3\sqrt{6}\cdot\sqrt{2}=6\sqrt{3}.
Из прямоугольного треугольника OPD
находим, что
OD=\sqrt{OP^{2}+DP^{2}}=\sqrt{6^{2}+(6\sqrt{3})^{2}}=12.
Источник: Вступительный экзамен в МФТИ. — 1996, билет 1, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 96-1-5, с. 356

