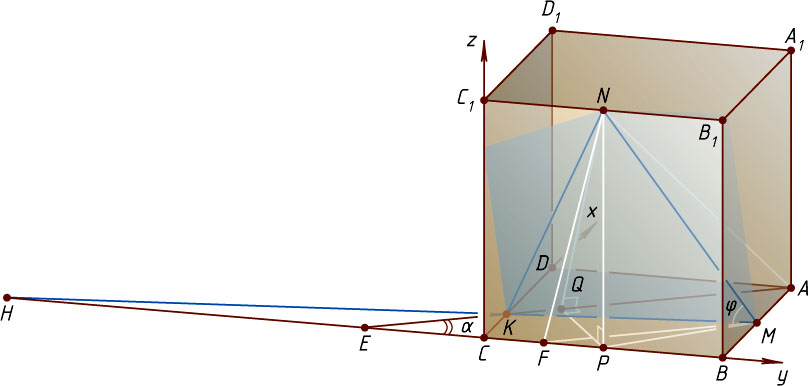
8735. В кубе ABCDA_{1}B_{1}C_{1}D_{1}
, ребро которого равно 6, точки M
и N
— середины рёбер AB
и B_{1}C_{1}
соответственно, а точка K
расположена на ребре DC
так, что DK=2\cdot KC
. Найдите
1) расстояние от точки N
до прямой AK
;
2) расстояние между прямыми MN
и AK
;
3) расстояние от точки A_{1}
до плоскости треугольника MNK
.
Ответ. 6\sqrt{\frac{17}{13}}
, \frac{18}{\sqrt{53}}
, \frac{66}{\sqrt{173}}
.
Решение. 1) Пусть P
— ортогональная проекция точки N
на плоскость основания ABCD
, а Q
— основание перпендикуляра, опущенного из точки P
на прямую AK
. По теореме о трёх перпендикулярах NQ\perp AK
, значит, расстояние от точки N
до прямой AK
равно длине отрезка NQ
.
Продолжим AK
и BC
до пересечения в точке E
. Из подобия треугольников KCE
и KDA
находим, что
CE=AD\cdot\frac{KC}{DK}=6\cdot\frac{2}{4}=3.
Обозначим \angle AEB=\alpha
. Тогда
\ctg\alpha=\frac{BE}{AB}=\frac{9}{6}=\frac{3}{2},~\sin\alpha=\frac{1}{\sqrt{1+\ctg^{2}\alpha}}=\frac{1}{\sqrt{1+\frac{9}{4}}}=\frac{2}{\sqrt{13}}.
Из прямоугольного треугольника PQE
находим, что
PQ=PE\sin\alpha=6\cdot\frac{2}{\sqrt{13}}=\frac{12}{\sqrt{13}}.
Следовательно,
NQ=\sqrt{NP^{2}+PQ^{2}}=\sqrt{6^{2}+\left(\frac{12}{\sqrt{13}}\right)^{2}}=\frac{6\sqrt{17}}{\sqrt{13}}.
2) Через точку M
проведём прямую, параллельную AK
. Пусть эта прямая пересекает BC
в точке F
. Тогда угол между прямыми MN
и AK
равен углу между прямыми MN
и MF
, а \angle BFM=\angle AEB=\alpha
. Из прямоугольного треугольника MBF
находим, что
BF=BM\ctg\angle BFM=3\ctg\alpha=\frac{9}{2},~MF=\frac{BM}{\sin\angle BFM}=\frac{MB}{\sin\alpha}=\frac{3}{\frac{2}{\sqrt{13}}}=\frac{3\sqrt{13}}{2}.
Тогда
PF=BF-BP=\frac{9}{2}-3=\frac{3}{2},~NF=\sqrt{NP^{2}+PF^{2}}=\sqrt{6^{2}+\left(\frac{3}{2}\right)^{2}}=\frac{3\sqrt{17}}{2}.
Кроме того,
PM=BM\sqrt{2}=3\sqrt{2},~MN=\sqrt{NP^{2}+PM^{2}}=\sqrt{6^{2}+(3\sqrt{2})^{2}}=3\sqrt{6}.
Рассмотрим треугольник MNF
. Обозначим \angle NMF=\varphi
. По теореме косинусов
\cos\varphi=\frac{MN^{2}+MF^{2}-NF^{2}}{2MN\cdot MF}=\frac{(3\sqrt{6})^{2}+\left(\frac{3\sqrt{13}}{2}\right)^{2}-\left(\frac{3\sqrt{17}}{2}\right)^{2}}{2\cdot3\sqrt{6}\cdot\frac{3\sqrt{13}}{2}}=\frac{5}{\sqrt{78}}.
Тогда
\sin\varphi=\sqrt{1-\cos^{2}\varphi}=\sqrt{1-\frac{25}{78}}=\sqrt{\frac{53}{78}}.
Из прямоугольного треугольника ADK
находим, что
AK=\sqrt{AD^{2}+DK^{2}}=\sqrt{36+16}=\sqrt{52}=2\sqrt{13}.
Пусть V
— объём тетраэдра AKMN
. Тогда, с одной стороны
V=\frac{1}{3}S_{\triangle AKM}\cdot NP=\frac{1}{3}\cdot\frac{1}{2}AM\cdot AD\cdot NP=\frac{1}{3}\cdot\frac{1}{2}\cdot3\cdot6\cdot6=18,
с другой стороны, если d
— искомое расстояние между прямыми AK
и MN
, то
V=\frac{1}{6}AK\cdot MN\cdot d\sin\varphi=\frac{1}{6}\cdot2\sqrt{13}\cdot3\sqrt{6}\cdot d\cdot\sqrt{\frac{53}{78}}=d\sqrt{53}.
Из уравнения d\sqrt{53}=18
находим, что d=\frac{18}{\sqrt{53}}
.
Это же расстояние можно найти с помощью метода координат. Выберем прямоугольную систему координат, приняв за начало точку C
, направив ось CX
по лучу CD
, ось CY
— по лучу CB
, а ось CZ
— по лучу CC_{1}
.
Пусть T
— точка пересечения прямых AK
и BC
, G
— точка пересечения прямых NF
и CC_{1}
. Поскольку CT=\frac{1}{3}MB=1
и CE=\frac{1}{2}BC=3
, уравнение плоскости MNF
имеет вид \frac{x}{-1}+\frac{y}{\frac{3}{2}}+\frac{z}{-6}=1
(уравнение плоскости в отрезках), или 6x-4y+z+6=0
. Расстояние между прямыми MN
и AK
равно расстоянию от точки A(6;6;0)
до плоскости MNF
, т. е.
d=\frac{|6\cdot6-4\cdot6+1\cdot0+6|}{\sqrt{6^{2}+4^{2}+1^{2}}}=\frac{18}{\sqrt{53}}.
3) Продолжим отрезок MK
до пересечения с прямой BC
в точке H
. Из подобия треугольников KCH
и MBH
находим, что
\frac{2}{3}=\frac{KC}{MB}=\frac{CH}{BH}=\frac{CH}{CH+BC}=\frac{CH}{CH+6},
откуда CH=12
.
Найдём координаты нужных нам точек: C(0;0;0)
, K(2;0;0)
, A_{1}(6;6;6)
, H(0;-12;0)
, N(0;3;6)
. Уравнение плоскости MNK
имеет вид \frac{x}{2}-\frac{y}{12}+\frac{z}{c}=1
(уравнение плоскости в отрезках), где (0;0;c)
— координаты точки пересечения плоскости MNK
с осью CZ
. Подставив в это уравнение координаты точки N
, найдём, что c=\frac{24}{5}
. Значит, уравнение плоскости ABC
—
\frac{x}{2}-\frac{y}{12}+\frac{5z}{24}=1~\Leftrightarrow~12x-2y+5z-24=0.
Пусть \rho
— искомое расстояние от точки A_{1}
до плоскости MNK
. По формуле расстояния от точки до плоскости находим, что
\rho=\frac{|12\cdot6-2\cdot6+5\cdot6-24|}{\sqrt{12^{2}+2^{2}+5^{2}}}=\frac{66}{\sqrt{173}}.
Источник: Вступительный экзамен в МФТИ. — 1996, билет 5, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 96-5-5, с. 359
