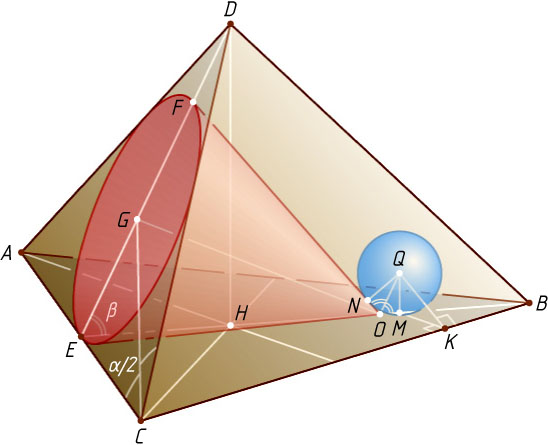
8739. В правильной треугольной пирамиде ABCD
сторона основания ABC
равна a
. Внутри пирамиды расположен конус, окружность основания которого вписана в треугольник ACD
, а вершиной конуса является точка O
, лежащая на высоте BE
треугольника ABC
, причём BE:OB=3
. Найдите радиус основания конуса и радиус шара, касающегося конуса и трёх граней пирамиды с общей точкой B
.
Ответ. \frac{a}{4}
; \frac{a\sqrt{13}(8-3\sqrt{3})}{74\sqrt{3}}
.
Решение. Пусть DH
— высота пирамиды, G
— центр основания конуса, r
— радиус основания конуса. Обозначим \angle ACD=\alpha
, \angle DEH=\beta
— угол боковой грани пирамиды с плоскостью основания. Из условия задачи следует, что
OE=\frac{2}{3}BE=\frac{2}{3}\cdot\frac{a\sqrt{3}}{2}=\frac{a}{\sqrt{3}}.
Из прямоугольных треугольников DEH
, DEB
, BEG
и OEG
находим, что
DE=\frac{EH}{\cos\angle DEH}=\frac{\frac{a}{2\sqrt{3}}}{\cos\beta}=\frac{a}{2\sqrt{3}\cos\beta},~DE=CE\tg\angle DBE=\frac{a}{2}\tg\alpha,
r=EG=BE\tg\angle EBG=\frac{a}{2}\tg\frac{\alpha}{2},~r=EG=OE\cos\angle OEG=\frac{a}{\sqrt{3}}\cos\beta.
Из равенств
\frac{a}{2\sqrt{3}\cos\beta}=\frac{a}{2}\tg\alpha,~\frac{a}{2}\tg\frac{\alpha}{2}=\frac{a}{\sqrt{3}}\cos\beta,
следует, что
\tg\alpha=\frac{1}{\sqrt{3}\cos\beta},~\tg\frac{\alpha}{2}=\frac{2\cos\beta}{\sqrt{3}}.
Подставив найденные выражения для \tg\alpha
и \tg\frac{\alpha}{2}
в формулу \tg\alpha=\frac{2\tg\frac{\alpha}{2}}{1-\tg^{2}\frac{\alpha}{2}}
, найдём, что \cos\beta=\frac{\sqrt{3}}{4}
. Следовательно
r=OE\cos\angle OEG=\frac{a}{\sqrt{3}}\cdot\cos\beta=\frac{a}{\sqrt{3}}\cdot\frac{\sqrt{3}}{4}=\frac{a}{4}.
Пусть x
— радиус шара, касающегося конуса и трёх граней пирамиды с общей точкой B
, Q
— центр шара, M
и N
— точки касания шара соответственно с плоскостью основания пирамиды и с образующей конуса. Тогда точка M
лежит на отрезке OB
. Рассмотрим сечение пирамиды плоскостью DBE
. Получим окружность радиуса x
с центром Q
, вписанную в угол NOB
. Поскольку центр окружности, вписанной в угол, лежит на биссектрисе этого угла, луч OQ
— биссектриса внешнего угла при вершине O
равнобедренного треугольника EOF
(F
— вторая общая точка вписанной окружности треугольника ABD
и его высоты DE
), поэтому \angle MOQ=\angle NOQ=\beta
. Из прямоугольного треугольника MOB
находим, что
OM=\frac{QM}{\tg\angle MOQ}=\frac{x}{\tg\beta}.
Из точки M
опустим перпендикуляр MK
на прямую BC
. По теореме о трёх перпендикулярах QK\perp BC
, а так как центр сферы, вписанной в двугранный угол, лежит в биссекторной плоскости этого угла, то \angle QKM=\frac{\beta}{2}
. Из прямоугольных треугольников QMK
и BMK
находим, что
MK=QM\ctg\angle QKM=xc\tg\frac{\beta}{2},~MB=2MK=2x\ctg\frac{\beta}{2}.
Учитывая, что \cos\beta=\frac{\sqrt{3}}{4}
и \cos\beta=\frac{1-\tg^{2}\frac{\beta}{2}}{1+\tg^{2}\frac{\beta}{2}}
, из уравнения
\frac{\sqrt{3}}{4}=\frac{1-\tg^{2}\frac{\beta}{2}}{1+\tg^{2}\frac{\beta}{2}}
находим, что \tg\frac{\beta}{2}=\frac{4-\sqrt{3}}{\sqrt{13}}
. Тогда
\ctg\frac{\beta}{2}=\frac{\sqrt{13}}{4-\sqrt{3}}=\frac{4+\sqrt{3}}{\sqrt{13}},
\tg\beta=\sqrt{\frac{1}{\cos^{2}\beta}-1}=\sqrt{\frac{16}{3}-1}=\frac{\sqrt{13}}{\sqrt{3}},~\ctg\beta=\frac{\sqrt{3}}{\sqrt{13}}
а так как OM+BM=OB
, то получаем уравнение
x\ctg\beta+2x\ctg\frac{\beta}{2}=\frac{a}{2\sqrt{3}},
из которого находим, что
x=\frac{a}{2\sqrt{3}\left(\ctg\beta+2\ctg\frac{\beta}{2}\right)}=\frac{a}{2\sqrt{3}\left(\frac{\sqrt{3}}{\sqrt{13}}+\frac{2(4+\sqrt{3})}{\sqrt{13}}\right)}=\frac{a\sqrt{13}}{2\sqrt{3}(8+3\sqrt{3})}=\frac{a\sqrt{13}(8-3\sqrt{3})}{74\sqrt{3}}.
Источник: Вступительный экзамен в МФТИ. — 1996, билет 9, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 96-9-5, с. 362
