8747. Сторона основания ABC
правильной треугольной призмы ABCA_{1}B_{1}C_{1}
равна 6, а высота равна \frac{3}{\sqrt{7}}
. На рёбрах AC
, A_{1}C_{1}
и BB_1
расположены соответственно точки P
, F
и K
так, что AP=1
, A_{1}F=3
и BK=KB_{1}
. Постройте сечение призмы плоскостью, проходящей через точки P
, F
и K
. Найдите площадь сечения и угол между плоскостью основания призмы и плоскостью сечения.
Ответ. \frac{39}{4}
; \frac{\pi}{6}
.
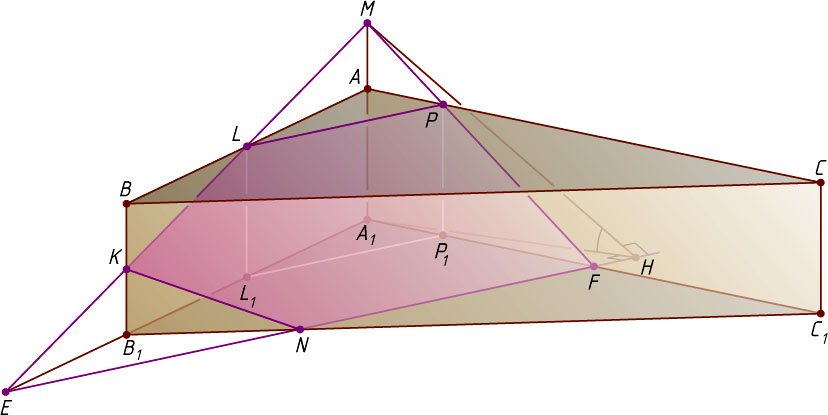
Решение. Пусть прямые FP
и AA_{1}
пересекаются в точке M
(рис. 1), прямая MK
пересекает прямые AB
и A_{1}B_{1}
в точках L
и E
соответственно, а прямые EF
и B_{1}C_{1}
пересекаются в точке N
. Тогда пятиугольник PLKNF
— искомое сечение.
Из подобия треугольников MAP
и MA_{1}F
находим, что
\frac{MA}{MA_{1}}=\frac{AP}{A_{1}F}=\frac{1}{3},
поэтому
MA=\frac{1}{2}AA_{1}=\frac{1}{2}\cdot\frac{3}{\sqrt{7}}=\frac{3}{2\sqrt{7}},MA_{1}=\frac{3}{2}AA_{1}=\frac{3}{2}\cdot\frac{3}{\sqrt{7}}=\frac{9}{2\sqrt{7}}.
Поскольку K
— середина BB_{1}
, BK=KB_{1}=AM
. Из равенства треугольников MAL
, KBL
и KB_{1}E
находим, что B_{1}E=BL=AL=3
.
Пусть H
— основание перпендикуляра, опущенного из точки A_{1}
на прямую EF
. Тогда по теореме о трёх перпендикулярах MH\perp FE
, значит, MFA_{1}
— линейный угол двугранного угла между секущей плоскостью и плоскостью основания призмы. По теореме косинусов
FE=\sqrt{A_{1}F^{2}+A_{1}E^{2}-2A_{1}F\cdot A_{1}E\cdot\cos60^{\circ}}=\sqrt{81+9-9\cdot3}=3\sqrt{7},
поэтому
S_{\triangle A_{1}FE}=\frac{1}{2}EF\cdot A_{1}H=\frac{1}{2}\cdot3\sqrt{7}\cdot A_{1}H=\frac{3\sqrt{7}}{2}A_{1}H.
С другой стороны,
S_{\triangle A_{1}FE}=\frac{1}{2}A_{1}F\cdot A_{1}E\sin60^{\circ}=\frac{1}{2}\cdot3\cdot9\cdot\frac{\sqrt{3}}{2}=\frac{27\sqrt{3}}{4}.
Из уравнения \frac{3\sqrt{7}}{2}A_{1}H=\frac{27\sqrt{3}}{4}
находим, что A_{1}H=\frac{9\sqrt{3}}{2\sqrt{7}}
. Следовательно,
\tg\angle MFA_{1}=\frac{MA_{1}}{A_{1}H}=\frac{\frac{9}{2\sqrt{7}}}{\frac{9\sqrt{3}}{2\sqrt{7}}}=\frac{1}{\sqrt{3}},~\angle MFA_{1}=30^{\circ}.
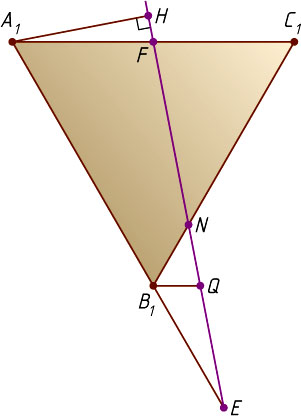
Через точку B_{1}
проведём прямую, параллельную A_{1}C_{1}
(рис. 2). Пусть эта прямая пересекается с прямой B_{1}C_{1}
в точке Q
. Из подобия треугольников EB_{1}Q
и EA_{1}F
следует, что
B_{1}Q=A_{1}F\cdot\frac{EB_{1}}{A_{1}F}=3\cdot\frac{3}{9}=1,
а из подобия треугольников NQB_{1}
и NFC_{1}
—
\frac{B_{1}N}{NC_{1}}=\frac{B_{1}Q}{FC_{1}}=\frac{1}{3}.
Пусть P_{1}
и L_{1}
— ортогональные проекции точек P
и L
на плоскость основания A_{1}B_{1}C_{1}
. Тогда A_{1}P_{1}=AP=1
и A_{1}L_{1}=AL=3
, пятиугольник P_{1}L_{1}B_{1}NF
— ортогональная проекция сечения PLKNF
на плоскость A_{1}B_{1}C_{1}
, а так как значит,
S_{P_{1}L_{1}B_{1}NF}=S_{\triangle A_{1}B_{1}C_{1}}-S_{\triangle A_{1}P_{1}L_{1}}-S_{\triangle C_{1}FN}=
=S_{\triangle A_{1}B_{1}C_{1}}-\frac{AP_{1}}{A_{1}C_{1}}\cdot\frac{A_{1}L_{1}}{A_{1}B_{1}}S_{\triangle A_{1}B_{1}C_{1}}-\frac{C_{1}F}{A_{1}C_{1}}\cdot\frac{C_{1}N}{C_{1}B_{1}}S_{\triangle A_{1}B_{1}C_{1}}=
=S_{\triangle A_{1}B_{1}C_{1}}-\frac{1}{6}\cdot\frac{1}{2}S_{\triangle A_{1}B_{1}C_{1}}-\frac{1}{2}\cdot\frac{3}{4}S_{\triangle A_{1}B_{1}C_{1}}=\frac{13}{24}S_{\triangle A_{1}B_{1}C_{1}}=
=\frac{13}{24}\cdot\frac{A_{1}B_{1}^{2}\sqrt{3}}{4}=\frac{13}{24}\cdot\frac{36\sqrt{3}}{4}=\frac{39\sqrt{3}}{8}.
Следовательно,
S_{PLBNF}=\frac{S_{P_{1}L_{1}B_{1}NF}}{\cos\angle MFA_{1}}=\frac{\frac{39\sqrt{3}}{8}}{\frac{\sqrt{3}}{2}}=\frac{39}{4}.
Источник: Вступительный экзамен в МФТИ. — 1998, билет 1, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 98-1-5, с. 374

