8751. Две противоположные боковые грани четырёхугольной пирамиды SABCD
перпендикулярны основанию, высота пирамиды равна \sqrt{5}
. В основании пирамиды лежит равнобедренная трапеция ABCD
(AD=BC
), описанная около окружности и такая, что AB=6
, \angle BAD=\frac{\pi}{3}
. Найдите расстояние от точки D
до плоскости SAB
.
Внутри пирамиды расположен конус так, что окружность его основания вписана в треугольник SCD
, а вершина принадлежит грани SAB
. Найдите объём конуса.
Ответ. \frac{\sqrt{30}}{4}
, \frac{\pi\sqrt{30}}{28}
.
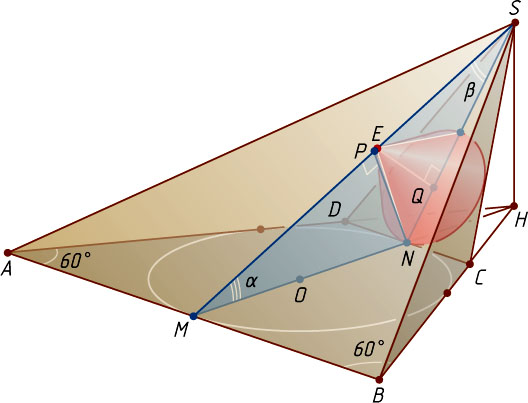
Решение. Поскольку плоскости противоположных боковых граней SAD
и SBC
(рис. 1) перпендикулярны плоскости основания пирамиды, прямая l
их пересечения также перпендикулярна плоскости основания и проходит через общую точку S
плоскостей SAD
и SBC
, а так как точка H
пересечения прямых AD
и BC
— также общая точка этих плоскостей, то прямая l
совпадает с прямой SH
, значит, SH
— высота пирамиды.
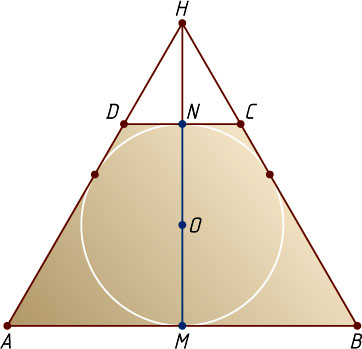
Окружность с центром O
, вписанная в равнобедренную трапецию ABCD
, является также вписанной окружностью равностороннего треугольника AHB
со стороной AB=6
. Если r
— радиус окружности, а M
и N
— середины AB
и CD
соответственно, то
MN=2r=2\cdot\frac{1}{3}HM=2\cdot\frac{1}{3}\cdot\frac{AB\sqrt{3}}{2}=2\cdot\frac{1}{3}\cdot\frac{6\sqrt{3}}{2}=2\sqrt{3}.
Прямая CD
параллельна прямой AB
, лежащей в плоскости ABS
, поэтому прямая CD
параллельна этой плоскости, значит, расстояние от точки D
до плоскости ABS
равно расстоянию до этой плоскости от любой точки прямой CD
, в частности, от точки N
. Пусть P
— основание перпендикуляра, опущенного из точки N
на прямую SM
. Поскольку прямая AB
перпендикулярна пересекающимся прямым HM
и SM
плоскости SMH
, прямая AB
перпендикулярна плоскости SNM
, значит, PN\perp AB
и NP
— перпендикуляр к плоскости ASB
. Следовательно, расстояние от точки D
до плоскости SAB
равно длине отрезка NP
.
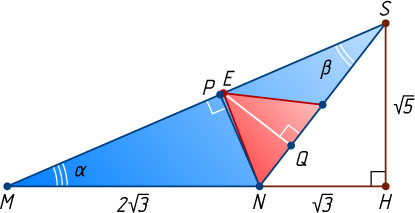
Рассмотрим прямоугольный треугольник SMH
(рис. 3). Обозначим \angle SMH=\alpha
. Тогда
\ctg\alpha=\frac{MH}{SH}=\frac{3\sqrt{3}}{\sqrt{5}},~\sin\alpha=\frac{1}{\sqrt{1+\ctg^{2}\alpha}}=\frac{1}{\sqrt{1+\frac{27}{5}}}=\frac{\sqrt{5}}{4\sqrt{2}}.
Следовательно,
PN=MN\sin\alpha=2\sqrt{3}\cdot\frac{\sqrt{5}}{4\sqrt{2}}=\frac{\sqrt{30}}{4}.
Из подобия треугольников DHC
и AHB
находим, что
CD=AB\cdot\frac{HN}{HM}=6\cdot\frac{1}{3}=2.
Тогда
HC=HD=CD=2,~SD=SC=\sqrt{SH^{2}+HC^{2}}=\sqrt{5+4}=3.
Из прямоугольных треугольников SHM
и SHN
находим, что
SM=\sqrt{SH^{2}+MH^{2}}=\sqrt{5+27}=4\sqrt{2},~SN=\sqrt{SH^{2}+NH^{2}}=\sqrt{5+3}=2\sqrt{2}.
Пусть Q
— центр окружности основания конуса, о котором говорится в условии задачи, R
— радиус этой окружности, p
— полупериметр треугольника CSD
. Так как окружность основания конуса есть вписанная окружность треугольника CSD
, то
R=\frac{S_{\triangle CSD}}{p}=\frac{\frac{1}{2}CD\cdot SN}{\frac{SC+DS+CD}{2}}=\frac{2\sqrt{2}}{4}=\frac{\sqrt{2}}{2}.
Пусть перпендикуляр, восставленный точки Q
к отрезку SN
, пересекает отрезок SM
в точке E
. Тогда EQ
— высота конуса. Обозначим \angle MSN=\beta
(рис. 3). По теореме косинусов
\cos\beta=\frac{SM^{2}+SN^{2}-MN^{2}}{2SM\cdot SN}=\frac{(4\sqrt{2})^{2}+(2\sqrt{2})^{2}-(2\sqrt{3})^{2}}{2\cdot4\sqrt{2}\cdot2\sqrt{2}}=\frac{7}{8}.
Тогда
\tg\beta=\sqrt{\frac{1}{\cos^{2}\beta}-1}=\sqrt{\frac{64}{49}-1}=\frac{\sqrt{15}}{7}.
Из прямоугольного треугольника SQE
находим, что
EQ=SQ\tg\beta=\frac{3\sqrt{2}}{2}\cdot\frac{\sqrt{15}}{7}=\frac{3\sqrt{30}}{14}.
Пусть V
— объём конуса. Тогда
V=\frac{1}{3}\pi R^{2}\cdot EQ=\frac{1}{3}\pi\cdot\left(\frac{\sqrt{2}}{2}\right)^{2}\cdot\frac{3\sqrt{30}}{14}=\frac{\pi\sqrt{30}}{28}.
Источник: Вступительный экзамен в МФТИ. — 1998, билет 5, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 98-5-5, с. 377


