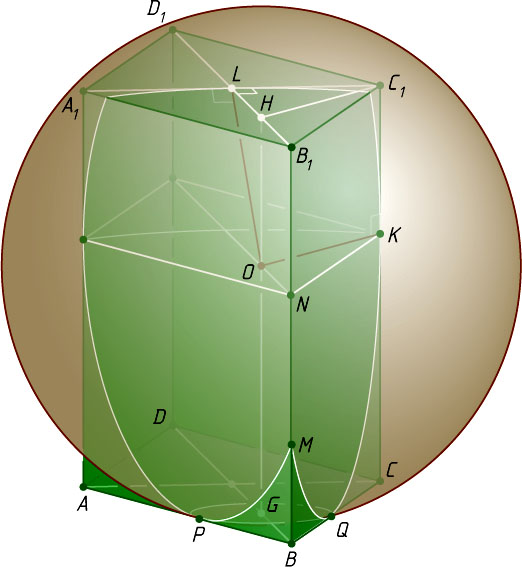
8755. В основании прямой призмы ABCDA_{1}B_{1}C_{1}D_{1}
лежит ромб ABCD
с углом BAD
, равным 2\arccos\frac{1}{3}
. Сфера касается всех звеньев ломаной ABCC_{1}A_{1}
и пересекает ребро BB_{1}
в точках B_{1}
и M
. Найдите объём призмы и радиус сферы, если B_{1}M=1
.
Ответ. V=\frac{4}{3}\sqrt{2}
, R=\frac{\sqrt{3}}{2}
.
Решение. Пусть сфера радиуса R
касается звеньев AB
, BC
, CC_{1}
, C_{1}A_{1}
ломаной ABCC_{1}A_{1}
в точках P
, Q
, K
и L
соответственно. Точки P
и Q
лежат на сфере, поэтому центр O
сферы лежит в плоскости, перпендикулярной отрезку PQ
и проходящей через его середину, а так как призма прямая и её основание — ромб, то эта плоскость совпадает с плоскостью BB_{1}D_{1}D
. В то же время, поскольку сфера проходит через точки B_{1}
и M
, её центр лежит в плоскости, перпендикулярной отрезку B_{1}M
и проходящей через его середину N
. Эти две плоскости пересекаются по прямой ON
, параллельной BD
.
Пусть L'
— центр ромба A_{1}B_{1}C_{1}D_{1}
. Прямая A_{1}C_{1}
перпендикулярна плоскости BB_{1}D_{1}D
, поэтому OL'\perp A_{1}C_{1}
. В то же время, радиус сферы, проведённый в точку L
касания сферы с прямой A_{1}C_{1}
, также перпендикулярен A_{1}C_{1}
, следовательно точки L'
и L
совпадают.
Пусть прямая, проходящая через точку O
параллельно боковому ребру призмы, пересекает диагонали B_{1}D_{1}
и BD
оснований в точках H
и G
соответственно. Поскольку OK\perp CC_{1}
(как радиус сферы, проведённый в точку касания сферы со звеном CC_{1}
), четырёхугольник OHC_{1}K
— прямоугольник, поэтому
C_{1}K=OH=B_{1}N=\frac{1}{2}B_{1}M=\frac{1}{2}.
Тогда C_{1}L=C_{1}K=\frac{1}{2}
как отрезки касательных, проведённых к сфере из одной точки C_{1}
.
Пусть высота призмы равна h
. Тогда
CQ=CK=CC_{1}-C_{1}K=h-\frac{1}{2},~BM=BB_{1}-B_{1}M=h-1.
По теореме о касательной и секущей
BQ=\sqrt{BB_{1}\cdot BM}=\sqrt{h(h-1)}.
Тогда
B_{1}C_{1}=BC=BQ+QC=\sqrt{h(h-1)}+h-\frac{1}{2}.
С другой стороны, из прямоугольного треугольника C_{1}LB_{1}
находим, что
B_{1}C_{1}=\frac{C_{1}L}{\cos\angle B_{1}C_{1}L}=\frac{C_{1}L}{\cos\frac{1}{2}\angle B_{1}C_{1}D_{1}}=\frac{\frac{1}{2}}{\frac{1}{3}}=\frac{3}{2}.
Таким образом, получим уравнение
\sqrt{h(h-1)}+h-\frac{1}{2}=\frac{3}{2},
из которого находим, что h=\frac{4}{3}
. Тогда
BP=BQ=\sqrt{h(h-1)}=\sqrt{\frac{4}{3}\cdot\frac{1}{3}}=\frac{2}{3},~CK=h-\frac{1}{2}=\frac{4}{3}-\frac{1}{2}=\frac{5}{6}.
Обозначим \angle BAD=\alpha
. По условию \cos\frac{\alpha}{2}=\frac{1}{3}
, поэтому
\sin\frac{\alpha}{2}=\sqrt{1-\frac{1}{9}}=\frac{2\sqrt{2}}{3},~\sin\alpha=2\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}=2\cdot\frac{2\sqrt{2}}{3}\cdot\frac{1}{3}=\frac{4\sqrt{2}}{9}.
Следовательно,
V_{ABCDA_{1}B_{1}C_{1}D_{1}}=S_{ABCD}\cdot h=AB\cdot AD\sin\alpha\cdot h=\left(\frac{3}{2}\right)^{2}\cdot\frac{4\sqrt{2}}{9}\cdot\frac{4}{3}=\frac{4}{3}\sqrt{2}.
Наконец, из прямоугольных треугольников BPG
и OPG
находим, что
PG=BP\ctg\angle PGB=BQ\ctg\frac{\alpha}{2}=\frac{2}{3}\cdot\frac{1}{2\sqrt{2}}=\frac{1}{3\sqrt{2}},
R^{2}=OP^{2}=\sqrt{PG^{2}+OG^{2}}=\sqrt{PG^{2}+CK^{2}}=\sqrt{\left(\frac{1}{3\sqrt{2}}\right)^{2}+\left(\frac{5}{6}\right)^{2}}=\frac{\sqrt{3}}{2}.
Источник: Вступительный экзамен в МФТИ. — 1994, билет 1, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 94-1-4, с. 338
