8759. В правильной четырёхугольной пирамиде SABCD
ребро AB
вдвое больше высоты пирамиды. По одну сторону от плоскости грани ABCD
расположен цилиндр, окружность основания которого проходит через центр этой грани. Ортогональные проекции цилиндра на плоскости SCD
и SBC
— прямоугольники с общей вершиной в точке C
. Найдите отношение объёмов цилиндра и пирамиды.
Ответ. \frac{\pi}{\sqrt{3}}
.
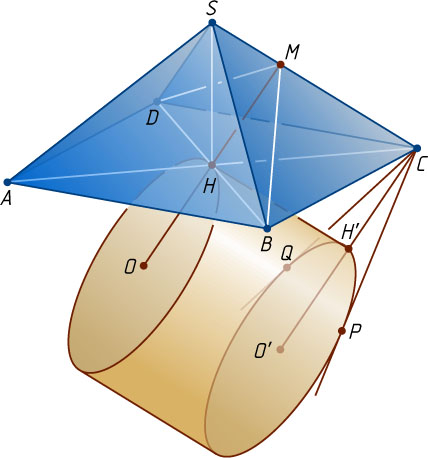
Решение. Поскольку цилиндр расположен по одну сторону от плоскости основания ABCD
и окружность его основания проходит через центр H
основания пирамиды, то H
— единственная общая точка окружности основания цилиндра и плоскости основания пирамиды (рис. 1).
Поскольку проекция цилиндра на плоскость SBC
есть прямоугольник, ось цилиндра параллельна этой плоскости. Аналогично, ось цилиндра параллельна плоскости SCD
. Следовательно, ось цилиндра параллельна прямой SC
пересечения этих плоскостей. Тогда плоскости оснований цилиндра перпендикулярны ребру SC
. По теореме о трёх перпендикулярах прямая BD
также перпендикулярна этому ребру и проходит через точку H
, лежащую в плоскости одного из оснований цилиндра. Значит, прямая BD
лежит в плоскости этого основания цилиндра, а так как H
— единственная общая точка окружности основания цилиндра и прямой BD
, то BD
— касательная к этой окружности.
Пусть M
— основание перпендикуляра, опущенного из центра H
квадрата ABCD
на ребро CS
. Точка M
лежит в одной из плоскостей оснований цилиндра, а плоскость второго основания проходит через точку C
, так как эта точка лежит на ортогональных проекциях второго основания на плоскости SCD
и SBC
. Значит, высота цилиндра равна длине отрезка MC
. Кроме того, цилиндр и вершина S
расположены по разные стороны от плоскости основания пирамиды, а в плоскости BMD
центр O
основания цилиндра и точка M
расположены по разные стороны от прямой BD
.
Обозначим AB=a
. Тогда SH=\frac{a}{2}
. Из прямоугольных треугольников SHC
, CMH
и DMH
находим, что
SC=\sqrt{CH^{2}+SH^{2}}=\sqrt{\left(\frac{a}{\sqrt{2}}\right)^{2}+\left(\frac{a}{2}\right)^{2}}=\frac{a\sqrt{3}}{2},
MH=\frac{CH\cdot SH}{CS}=\frac{\frac{a}{\sqrt{2}}\cdot\frac{a}{2}}{\frac{a\sqrt{3}}{2}}=\frac{a}{\sqrt{6}},
CM=\sqrt{CH^{2}-MH^{2}}=\sqrt{\left(\frac{a}{\sqrt{2}}\right)^{2}-\left(\frac{a}{\sqrt{6}}\right)^{2}}=\frac{a}{\sqrt{3}},
\tg\angle DMH=\frac{DH}{MH}=\frac{\frac{a}{\sqrt{2}}}{\frac{a}{\sqrt{6}}}=\sqrt{3},~\angle DMH=60^{\circ},~\angle BMD=2\angle DMH=120^{\circ}.
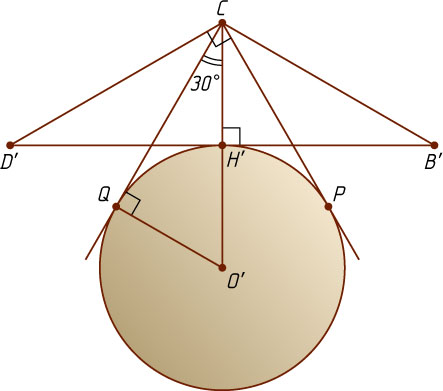
Рассмотрим плоскость, проходящую через точку C
перпендикулярно ребру SC
(рис. 2). В этой плоскости расположена окружность основания цилиндра и две касательные к ней — прямые, содержащие стороны прямоугольников с общей вершиной C
. Одна из этих прямых перпендикулярна плоскости SCD
, а вторая — плоскости SBC
. Пусть P
и Q
— точки касания, а B'
, D'
, H'
и O'
— ортогональные проекции на эту плоскость точек B
, D
, H
и O
соответственно. Тогда \angle O'CB'=\angle O'CD'=\angle OMD=60^{\circ}
, а \angle PCD'=\angle QCB'=90^{\circ}
, так как прямые PC
и QC
перпендикулярны плоскостям SCD
и SCB
, содержащим прямые CD'
и CB'
соответственно. Поэтому
\angle O'CQ=\angle QCB'-\angle O'CB'=90^{\circ}-60^{\circ}=30^{\circ}.
Пусть R
— радиус основания цилиндра. Из прямоугольного треугольника O'CQ
находим, что
R=O'Q=\frac{1}{2}O'C=\frac{1}{2}(O'H'+CH')=\frac{1}{2}(R+CH')=\frac{1}{2}\left(R+\frac{a}{\sqrt{6}}\right),
откуда R=\frac{a}{\sqrt{6}}
.
Если V_{1}
— объём цилиндра, а V_{1}
— объём пирамиды, то
V_{1}=\pi R^{2}\cdot MC=\frac{\pi a^{2}}{6}\cdot\frac{a}{\sqrt{3}}=\frac{\pi a^{3}}{6\sqrt{3}},~V_{2}=\frac{1}{3}a^{2}\cdot\frac{a}{2}=\frac{a^{3}}{6}.
Следовательно,
\frac{V_{1}}{V_{2}}=\frac{\frac{\pi a^{3}}{6\sqrt{3}}}{\frac{a^{3}}{6}}=\frac{\pi}{\sqrt{3}}.
Источник: Вступительный экзамен в МФТИ. — 1994, билет 5, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 94-5-4, с. 341

