8763. Сфера, касающаяся верхнего основания цилиндра, имеет единственную общую точку с окружностью его нижнего основания и делит ось цилиндра в отношении 2:6:1
, считая от центра одного из оснований. Найдите объём цилиндра, если известно, что сфера касается двух его образующих, находящихся на расстоянии 2\sqrt{6}
друг от друга.
Ответ. \frac{441}{8}\pi
.
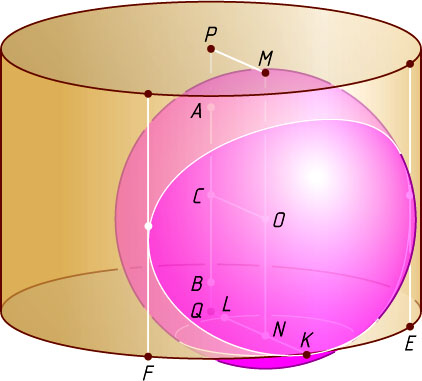
Решение. Пусть P
и Q
— центры верхнего и нижнего оснований цилиндра соответственно, O
— центр сферы, A
и B
— точки пересечения сферы с осью цилиндра, K
— единственная общая точка сферы и окружности нижнего основания цилиндра (рис. 1).
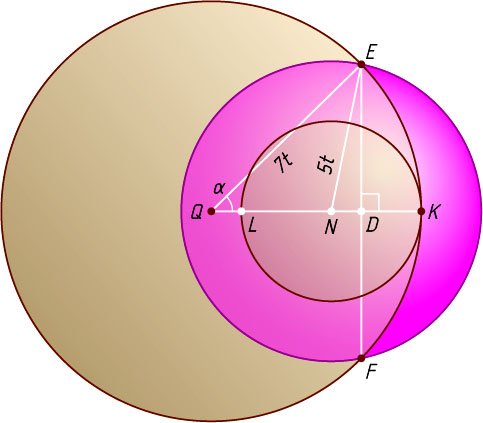
Рассмотрим сечение цилиндра и сферы плоскостью нижнего основания цилиндра (рис. 2). Получим окружность нижнего основания цилиндра и касающуюся её внутренним образом в точке K
окружность сечения сферы, причём центр N
этой окружности — ортогональная проекция центра O
сферы на эту плоскость. Точки Q
, N
и K
лежат на одной прямой, так как линия центров двух касающихся окружностей проходит через их точку касания.
Пусть M
— точка касания сферы с верхним основанием цилиндра. Тогда радиус OM
сферы перпендикулярен плоскости верхнего основания цилиндра, значит, точки O
, M
и N
лежат на одной прямой.
Рассмотрим сечение цилиндра и сферы плоскостью, проходящей через ось PQ
цилиндра и точку K
. Из предыдущих рассуждений следует, что в эта плоскость проходит через прямую MN
.
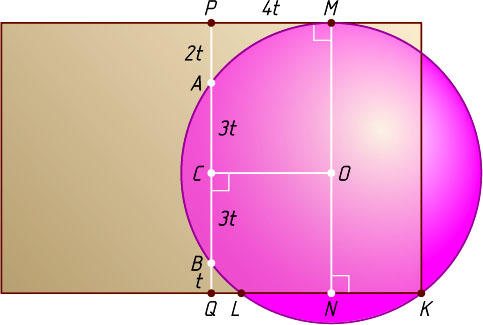
Пусть C
— проекция точки O
на прямую PQ
(рис. 3). Поскольку радиус, перпендикулярный хорде, делит её пополам, точка C
— середина отрезка AB
. Предположим, что PA:AB:BQ=1:6:2
. Тогда CQ\gt CP=OM=r
, где r
— радиус сферы, что невозможно, так как сфера пересекает нижнее основание цилиндра. Значит, PA:AB:BQ=2:6:1
.
Положим AP=2t
, AB=6t
, BQ=3t
. Тогда
PQ=2t+6t+t=9t,~r=OM=PC=PA+AC=2t+3t=5t.
По теореме о касательной и секущей
PM^{2}=PA\cdot PB=2t(2t+6t)=16t^{2},~PM=4t,
Пусть L
— отличная от K
точка пересечения окружности сечения с прямой QK
. Тогда N
— середина KL
и по теореме о касательной и секущей
7t^{2}=t\cdot7t=QB\cdot QA=QL\cdot QK=QB\cdot QA=(QN-LN)(QN+NK)=
=(PM-NL)(PM+NL)=(4t-NL)(4t+NL)=16t^{2}-NL^{2},
откуда NL=3t
. Если R
— радиус основания цилиндра, то
R=QK=QN+NK=PM+NK=PM+NL=4t+3t=7t.
Пусть E
и F
— проекции на плоскость нижнего основания цилиндра тех образующих цилиндра, которые касаются сферы. Тогда EF=2\sqrt{6}
, а так как QK
— серединный перпендикуляр к общей хорде EF
пересекающихся окружностей, то EF\perp QK
и точка D
пересечения EF
и QK
— середина отрезка EF
.
В треугольнике QEN
известно, что
QE=QK=R=7t,~NE=r=5t,~QN=PM=4t.
Обозначим \angle EQN=\alpha
. По теореме косинусов
\cos\alpha=\frac{QE^{2}+QN^{2}-NE^{2}}{2QE\cdot QN}=\frac{49t^{2}+16t^{2}-25t^{2}}{2\cdot7t\cdot4t}=\frac{5}{7},
тогда
\sin\alpha=\sqrt{1-\cos^{2}\alpha}=\sqrt{1-\frac{25}{49}}=\frac{2\sqrt{6}}{7}.
Из прямоугольного треугольника EDQ
находим, что
7t=QE=\frac{ED}{\sin\alpha}=\frac{\sqrt{6}}{\frac{2\sqrt{6}}{7}}=\frac{7}{2},
откуда t=\frac{1}{2}
. Следовательно, если V
— объём цилиндра, то
V=\pi R^{2}\cdot PQ=\pi\cdot49t^{2}\cdot9t=441\pi t^{3}=\frac{441\pi}{8}.
Источник: Вступительный экзамен в МФТИ. — 1994, билет 9, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 94-9-4, с. 344


