8767. В правильной четырёхугольной пирамиде SABCD
(S
— вершина) AB=3\sqrt{2}
, высота пирамиды равна 8. Сечения пирамиды двумя параллельными плоскостями, одна из которых проходит через точку A
, а другая — через точки B
и D
, имеют равные площади. В каком отношении делят ребро SC
плоскости сечений? Найдите расстояние между плоскостями сечений и объёмы многогранников, на которые пирамида разбивается этими плоскостями.
Ответ. 1:1:1
, \frac{12}{5}
, V_{1}=V_{2}=8
, V_{3}=32
.
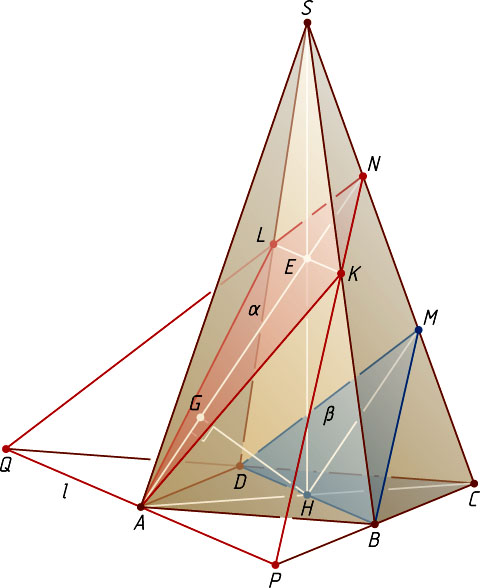
Решение. По теореме о пересечении двух параллельных плоскостей третьей плоскостью прямая l
пересечения плоскости \alpha
сечения, проходящей через точку A
, и плоскости основания параллельна прямой BD
. Пусть прямая l
пересекает прямые CB
и CD
в точках P
и Q
соответственно (рис. 1). Тогда BP=AD
как противоположные стороны параллелограмма ADBP
, поэтому BP=BC=3\sqrt{2}
. Аналогично DQ=DC=3\sqrt{2}
.
Пусть SH
— высота пирамиды. Поскольку в сечении пирамиды плоскостью \alpha
получается многоугольник, эта плоскость должна пересечь боковое ребро SC
в некоторой точке N
. Тогда параллельная ей плоскость \beta
, проходящая через прямую BD
, пересекает это ребро в некоторой точке M
, причём AN\parallel HM
как прямые пересечения параллельных плоскостей плоскостью ASC
. Поскольку H
— середина AC
, точка M
— середина отрезка CN
.
Сечение пирамиды плоскостью \beta
— равнобедренный треугольник BMD
. Пусть прямые PN
и SB
пересекаются в точке K
, а прямые QN
и SD
— в точке L
. Тогда четырёхугольник AKNL
— сечение пирамиды плоскостью \alpha
. Поскольку AC\perp BD
, то по теореме о трёх перпендикулярах AN\perp BD
, а так как KL\parallel BD
, то AN\perp KL
, т. е. диагонали четырёхугольника AKNL
взаимно перпендикулярны. Значит, S_{AKNL}=\frac{1}{2}AN\cdot KL
, а так как HM
— высота треугольника BMD
, то S_{\triangle BMD}=\frac{1}{2}BD\cdot HM
. По условию задачи \frac{1}{2}AN\cdot KL=\frac{1}{2}BD\cdot HM
.
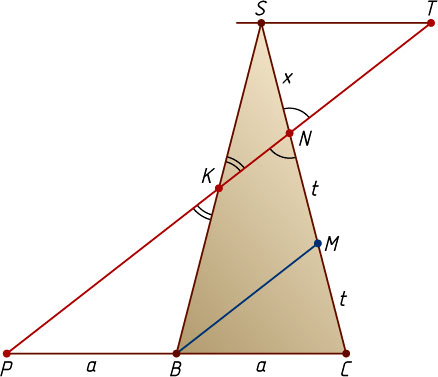
Рассмотрим сечение пирамиды плоскостью BSC
(рис. 2). Через вершину S
проведём прямую, параллельную BC
, и продолжим PN
до пересечения с этой прямой в точке T
. Обозначим CM=MN=t
, SN=x
, BP=BC=a
. Из подобия треугольников SNT
и CNP
следует, что
ST=PC\cdot\frac{SN}{NC}=2a\cdot\frac{x}{2t}=\frac{ax}{t},
а из подобия треугольников SKT
и BKP
—
\frac{SK}{KB}=\frac{ST}{BP}=\frac{\frac{ax}{t}}{a}=\frac{x}{t}.
Тогда из подобия треугольников SKL
и SBD
следует, что
KL=BD\cdot\frac{SK}{SB}=BD\cdot\frac{x}{x+t}.
Поэтому
\frac{1}{2}AN\cdot KL=\frac{1}{2}BD\cdot HM~\Leftrightarrow~AN\cdot KL=BD\cdot HM~\Leftrightarrow
\Leftrightarrow~AN\cdot BD\cdot\frac{x}{x+t}=BD\cdot\frac{1}{2}AN~\Leftrightarrow~\frac{x}{x+t}=\frac{1}{2}~\Leftrightarrow~x=t,
т. е. SN:NM:MC=1:1:1
.
Пусть E
— точка пересечения диагоналей сечения AKNL
. Тогда точка E
лежит на высоте SH
пирамиды. Обозначим AH=HC=b
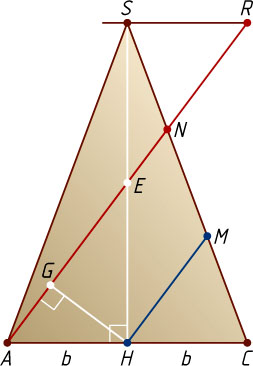
. Рассмотрим сечение пирамиды плоскостью ASC
(рис. 3). Через вершину S
проведём прямую, параллельную AC
, и продолжим AN
до пересечения с этой прямой в точке R
. Из подобия треугольников SNR
и CNA
следует, что
SR=AC\cdot\frac{SN}{NC}=2b\cdot\frac{1}{2}=b,
а из подобия треугольников SER
и HEA
—
\frac{SE}{EH}=\frac{SR}{AH}=\frac{b}{b}=1,
т. е. E
— середина SH
. Тогда K
— середина SB
и L
— середина SD
.
Пусть G
— основание перпендикуляра, опущенного из точки H
на AN
. Тогда GH
— перпендикуляр к плоскости \alpha
, опущенный из точки, лежащей в плоскости \beta
, параллельной \alpha
, значит, длина этого перпендикуляра равна расстоянию между плоскостями \alpha
и \beta
. Рассмотрим прямоугольный треугольник AHE
, в котором
AH=\frac{1}{2}AC=\frac{1}{2}\cdot3\sqrt{2}\cdot\sqrt{2}=3,~EH=\frac{1}{2}SH=4,~AE=\sqrt{16+9}=5.
Отрезок HG
— высота этого треугольника, проведённая из вершины прямого угла, следовательно,
HG=\frac{AH\cdot EH}{AE}=\frac{3\cdot4}{5}=\frac{12}{5}.
Пусть V
— объём пирамиды SABCD
, V_{1}
— объём треугольной пирамиды MBCD
, V_{2}
— объём четырёхугольной пирамиды SAKNL
, V_{3}
— объём части исходной пирамиды, заключённой между плоскостями \alpha
и \beta
. Тогда
V=\frac{1}{3}AB^{2}\cdot SH=\frac{1}{3}\cdot(3\sqrt{2})^{2}\cdot8=48,
V_{SBCD}=V_{SABD}=\frac{1}{2}V=24,~V_{1}=\frac{1}{3}V_{SBCD}=\frac{1}{2}\cdot24=8,
V_{2}=\frac{SA}{SA}\cdot\frac{SK}{SB}\cdot\frac{SL}{SD}V_{SABD}+\frac{SN}{SC}\cdot\frac{SK}{SB}\cdot\frac{SL}{SD}V_{SBCD}=
=\frac{1}{1}\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot24+\frac{1}{3}\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot24=6+2=8,
V_{3}=V-V_{1}-V_{2}=48-8-8=32.
Источник: Вступительный экзамен в МФТИ. — 1995, билет 1, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 95-1-4, с. 347


