8795. Ребро куба ABCDA_{1}B_{1}C_{1}D_{1}
равно 1. Найдите радиус сферы, касающейся:
а) рёбер BA
, BB_{1}
, BC
и плоскости A_{1}DC_{1}
;
б) рёбер BA
, BB_{1}
, BC
и прямой DA_{1}
.
Ответ. \frac{6\sqrt{2}-4\sqrt{3}}{3}
; 2\sqrt{2}-\sqrt{5}
.
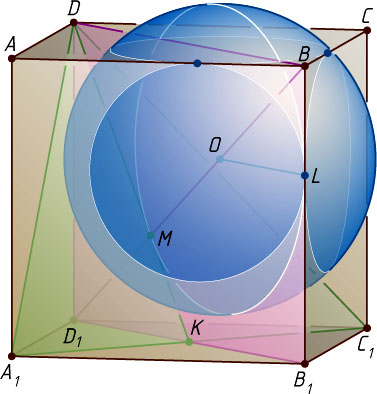
Решение. а) Центр O
сферы радиуса r
, касающейся рёбер BA
, BB_{1}
и BC
, лежит на луче BD_{1}
(рис. 1). Известно, что диагональ BD_{1}
куба ABCDA_{1}B_{1}C_{1}D_{1}
перпендикулярна плоскости A_{1}DC_{1}
, проходит через точку M
пересечения медиан треугольника A_{1}DC_{1}
и делится этой точкой в отношении 2:1
, считая от вершины B
, поэтому OM=r
и BM=\frac{2}{3}BD_{1}=\frac{2\sqrt{3}}{3}
.
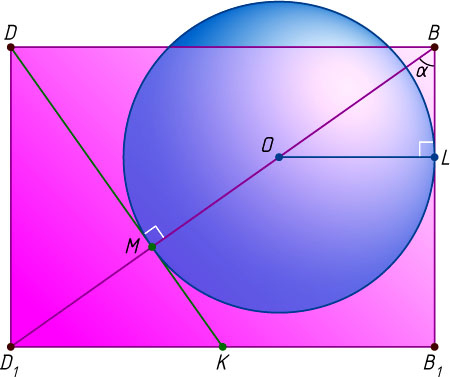
Рассмотрим сечение куба плоскостью BB_{1}D_{1}D
(рис. 2). Получим прямоугольник BB_{1}D_{1}D
со сторонами BB_{1}=1
, BD=\sqrt{2}
и диагональю BD_{1}=\sqrt{3}
, окружность радиуса r
с центром O
на диагонали BD_{1}
, касающуюся в точке M
отрезка DK
, соединяющего точку D
с серединой K
стороны B_{1}D_{1}
, а также касающуюся луча BB_{1}
в некоторой точке L
.
Обозначим \angle B_{1}BD_{1}=\alpha
. Тогда
\sin\alpha=\frac{B_{1}D_{1}}{BD_{1}}=\frac{\sqrt{2}}{\sqrt{3}},~OB=\frac{OL}{\sin\alpha}=r\sqrt{\frac{3}{2}}.
Заметим, что точка O
луча BD_{1}
лежит на отрезке BM
, а не на его продолжении, так как иначе сфера касалась бы не рёбер BA
, BB_{1}
и BC
, а их продолжений. Следовательно,
OM+OB=MB,~\mbox{или}~r+r\sqrt{\frac{3}{2}}=\frac{2\sqrt{3}}{3},
откуда находим, что r=\frac{6\sqrt{2}-4\sqrt{3}}{3}
.
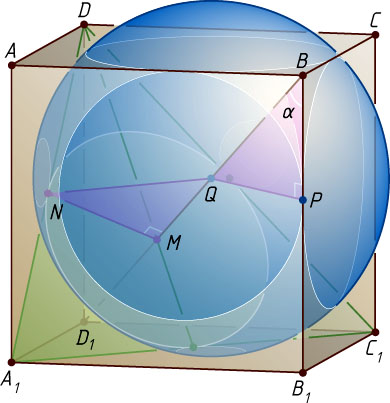
б) Пусть Q
— центр сферы радиуса R
, касающейся рёбер BA
, BB_{1}
, BC
и прямой DA_{1}
(рис. 3). Точка Q
также лежит на луче BD_{1}
. Рассмотрим сечение куба и сферы плоскостью A_{1}DC_{1}
. Получим равносторонний треугольник A_{1}DC_{1}
со стороной \sqrt{2}
и окружность с центром в точке M
, вписанную в этот треугольник. Если N
— точка касания окружности со стороной DA_{1}
, то MN=\frac{\sqrt{2}\cdot\sqrt{3}}{6}=\frac{1}{\sqrt{6}}
— радиус этой окружности. Обозначим QM=x
. Заметим, что точка Q
лежит на отрезке BM
, а не его продолжении. Из прямоугольного треугольника QMN
находим, что
R=QN=\sqrt{MN^{2}+QM^{2}}=\sqrt{\frac{1}{6}+x^{2}}.
С другой стороны, если сфера касается ребра BB_{1}
в точке P
, то QP=R
и из прямоугольного треугольника QPB
находим, что
R=QP=QB\sin\alpha=(BM-QM)\sin\alpha=\left(\frac{2\sqrt{3}}{3}-x\right)\cdot\frac{\sqrt{2}}{\sqrt{3}}.
Из уравнения
\sqrt{\frac{1}{6}+x^{2}}=\left(\frac{2\sqrt{3}}{3}-x\right)\cdot\frac{\sqrt{2}}{\sqrt{3}}
находим, что x=\frac{3\sqrt{30}-8\sqrt{3}}{6}
. Следовательно,
R=\left(\frac{2\sqrt{3}}{3}-x\right)\cdot\frac{\sqrt{2}}{\sqrt{3}}=\left(\frac{2\sqrt{3}}{3}-\frac{3\sqrt{30}-8\sqrt{3}}{6}\right)\cdot\frac{\sqrt{2}}{\sqrt{3}}=
=2\sqrt{2}-\sqrt{5}.
Источник: Вступительный экзамен в МФТИ. — 2003, билет 5, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 03-5-1, с. 419


