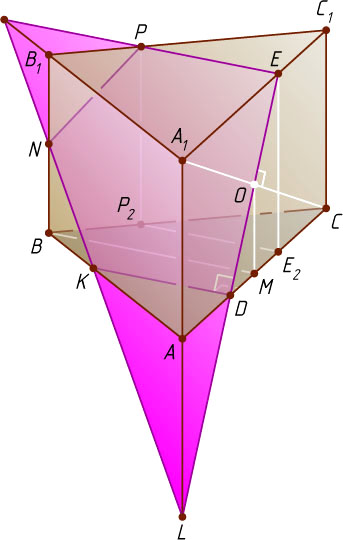
8921. Основание прямой призмы ABCA_{1}B_{1}C_{1}
— равнобедренный треугольник ABC
, в котором AB=BC=5
, \angle ABC=2\arcsin\frac{3}{5}
. Плоскость, перпендикулярная прямой A_{1}C
, пересекает рёбра AC
и A_{1}C_{1}
в точках D
и E
соответственно, причём AD=\frac{1}{3}AC
, EC_{1}=\frac{1}{3}A_{1}C_{1}
. Найдите площадь сечения призмы этой плоскостью.
Ответ. \frac{40}{3}
; сечение — пятиугольник.
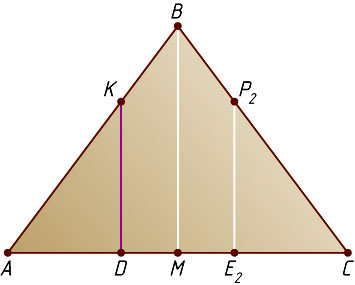
Решение. Пусть M
— середина основания AC
равнобедренного треугольника ABC
(рис. 2). Из прямоугольного треугольника AMB
находим, что
AM=AB\sin\angle ABM=5\cdot\frac{3}{5}=3,~BM=\sqrt{AB^{2}-AM^{2}}=\sqrt{25-9}=4.
Тогда
AC=2AM=6,~AD=\frac{1}{3}AC=2,~C_{1}E=\frac{1}{3}A_{1}C_{1}=2.
Поскольку прямая A_{1}C
перпендикулярна секущей плоскости (рис. 1), A_{1}C\perp DE
. Пусть O
— точка пересечения отрезков A_{1}C
и DE
. Из равенства прямоугольных треугольников A_{1}OE
и COD
(по гипотенузе и острому углу) следует, что O
— середина A_{1}C
, поэтому, перпендикуляр, опущенный из точки O
на AC
проходит через точку M
, а так как призма прямая, то этот перпендикуляр лежит в плоскости грани AA_{1}C_{1}C
.
Пусть K
— точка пересечения секущей плоскости с прямой AB
. Прямая A_{1}C
перпендикулярна секущей плоскости, содержащей прямую DK
, поэтому A_{1}C\perp DK
. По теореме о трёх перпендикулярах DK\perp AC
, так как AC
— ортогональная проекция наклонной A_{1}C
на плоскость ABC
. Треугольники ADK
и AMB
подобны с коэффициентом k=\frac{AD}{AM}=\frac{2}{3}
, поэтому
AK=AB\cdot\frac{AD}{AM}=\frac{2}{3}AB\lt AB,
значит, точка K
лежит на отрезке AB
. Аналогично, точка P
пересечения секущей плоскости с прямой B_{1}C_{1}
лежит на ребре B_{1}C_{1}
. При этом EP\parallel DK
и EP=DK
.
Пусть прямые ED
и AA_{1}
пересекаются в точке L
, прямые LK
и BB_{1}
— в точке N
. Тогда сечение призмы, о котором говорится в условии задачи, — пятиугольник DKNPE
. Его ортогональная проекция на плоскость ABC
— пятиугольник DKBP_{2}E_{2}
(рис. 2), где P_{2}
и E_{2}
— ортогональные проекции на плоскость ABC
точек P
и E
. Тогда
S_{\triangle CE_{2}P_{2}}=S_{\triangle ADK}=k^{2}S_{AMB}=k^{2}\cdot\frac{1}{2}AM\cdot BM=\left(\frac{2}{3}\right)^{2}\cdot\frac{1}{2}\cdot3\cdot4=\frac{8}{3},
S_{DKBP_{2}E_{2}}=S_{\triangle ABC}-2S_{\triangle ADK}=\frac{1}{2}AC\cdot BM-2S_{\triangle ADK}=\frac{1}{2}\cdot6\cdot4-2\cdot\frac{8}{3}=\frac{20}{3}.
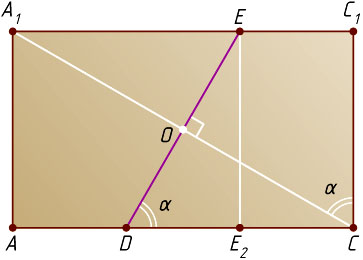
Пусть h
— высота (боковое ребро) призмы. Рассмотрим грань AA_{1}C_{1}C
(рис. 3). Обозначим \angle A_{1}CC_{1}=\angle EDE_{2}=\alpha
. Из прямоугольных треугольников CA_{1}C_{1}
и DEE_{2}
находим, что \tg\alpha=\frac{A_{1}C_{1}}{CC_{1}}=\frac{6}{h}
и \tg\alpha=\frac{EE_{2}}{DE_{2}}=\frac{h}{2}
, откуда h=2\sqrt{3}
и \tg\alpha=\sqrt{3}
. Поэтому \alpha=60^{\circ}
.
Поскольку CD\perp KD
и ED\perp KD
, угол EDC
— линейный угол двугранного угла между секущей плоскостью и плоскостью ABC
, а так как \angle EDC=\alpha=60^{\circ}
, то по теореме о площади ортогональной проекции многоугольника
S_{DKNPE}=\frac{S_{DKBP_{2}E_{2}}}{\cos\alpha}=\frac{\frac{20}{3}}{\frac{1}{2}}=\frac{40}{3}.
Источник: Вступительный экзамен в МФТИ. — 1992, билет 9, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 92-9-4, с. 324


