8925. Ребро правильного тетраэдра ABCD
равно a
, точка K
— середина ребра AB
, точка E
лежит на ребре CD
и EC:ED=1:2
, точка F
— центр грани ABC
. Найдите угол между прямыми BC
и KE
, расстояние между этими прямыми и радиус сферы, проходящей через точки A
, B
, E
и F
.
Ответ. \arccos\frac{7}{2\sqrt{19}}
, \frac{a\sqrt{6}}{9}
, a\sqrt{\frac{11}{6}}
.
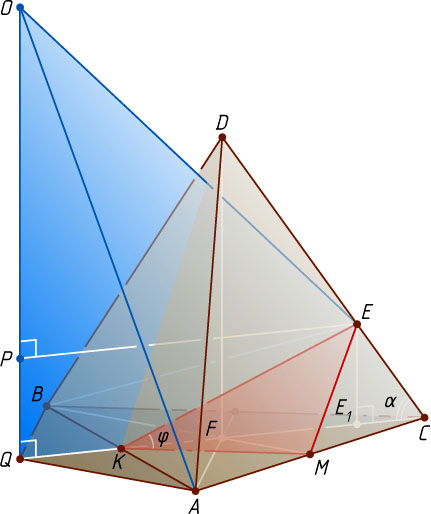
Решение. Через точку K
проведём прямую, параллельную ребру BC
(рис. 1). Пусть эта прямая пересекает ребро AC
в точке M
. Тогда M
— середина ребра AC
, KM=\frac{1}{2}BC=\frac{1}{2}a
.
По определению угла между скрещивающимися прямыми угол между прямыми BC
и KE
равен углу между пересекающимися прямыми KM
и KE
. Обозначим \angle EKM=\varphi
, \angle DCF=\alpha
. Из прямоугольного треугольника CFD
находим, что
\cos\alpha=\frac{CF}{CD}=\frac{\frac{a}{\sqrt{3}}}{a}=\frac{1}{\sqrt{3}}.
По теореме косинусов
EM^{2}=CE^{2}+CM^{2}-2CE\cdot CM\cos60^{\circ}=\frac{1}{9}a^{2}+\frac{1}{4}a^{2}-2\cdot\frac{1}{3}a\cdot\frac{1}{2}a\cdot\frac{1}{2}=\frac{7}{36}a^{2},
KE^{2}=CE^{2}+CK^{2}-2CE\cdot CK\cos\alpha=\frac{1}{9}a^{2}+\frac{3}{4}a^{2}-2\cdot\frac{1}{3}a\cdot\frac{a\sqrt{3}}{2}\cdot\frac{1}{\sqrt{3}}=\frac{19}{36}a^{2}.
Следовательно,
\cos\varphi=\frac{KE^{2}+KM^{2}-EM^{2}}{2KE\cdot KM}=\frac{\frac{19}{36}a^{2}+\frac{1}{4}a^{2}-\frac{7}{36}a^{2}}{2\cdot\frac{\sqrt{19}}{6}a\cdot\frac{1}{2}a}=\frac{7}{2\sqrt{19}}.
Тогда
\sin\varphi=\sqrt{1-\cos^{2}\varphi}=\sqrt{1-\frac{49}{76}}=\frac{3\sqrt{3}}{2\sqrt{19}}.
Пусть V
— объём тетраэдра ABCD
. Тогда
V=\frac{1}{3}S_{\triangle ABC}\cdot DF=\frac{1}{3}\cdot\frac{a^{2}\sqrt{3}}{4}\cdot a\sqrt{\frac{2}{3}}=\frac{a^{3}\sqrt{2}}{12}.
Тогда, если E_{1}
— ортогональная проекция точки E
на плоскость ABC
, то
V_{BCKE}=\frac{1}{3}S_{\triangle BCK}\cdot EE_{1}=\frac{1}{3}\cdot\frac{1}{2}S_{\triangle ABC}\cdot\frac{1}{3}DF=\frac{1}{6}\cdot\left(\frac{1}{3}S_{\triangle ABC}\cdot DF\right)=\frac{1}{6}V=\frac{a^{3}\sqrt{2}}{72}.
С другой стороны, если d
— расстояние между прямыми BC
и KE
, то
V_{BCKE}=\frac{1}{6}BC\cdot KE\cdot d\cdot\sin\varphi=\frac{1}{6}\cdot a\cdot\frac{a\sqrt{19}}{6}\cdot d\cdot\frac{3\sqrt{3}}{2\sqrt{19}}=\frac{a^{2}d\sqrt{3}}{24}.
Из уравнения \frac{a^{2}d\sqrt{3}}{24}=\frac{a^{3}\sqrt{2}}{72}
находим, что d=\frac{a\sqrt{6}}{9}
.
Центр O
сферы радиуса R
, проходящей через точки A
, B
, E
и F
, лежит на прямой, перпендикулярной плоскости ABF
и проходящей через центр Q
окружности, описанной около треугольника ABF
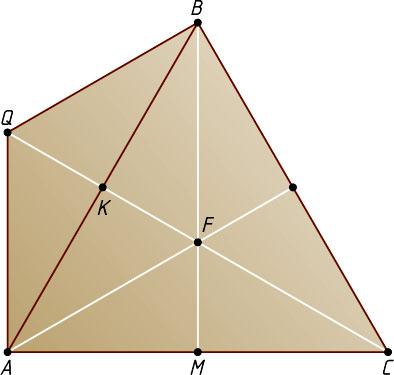
. Заметим (рис. 2), что Q
— точка, симметричная точке F
относительно прямой AB
(так как QA=QB=QF=FC=\frac{a}{\sqrt{3}}
). Обозначим OQ=x
. Из прямоугольного треугольника AQO
находим, что
R^{2}=OA^{2}=OQ^{2}+AQ^{2}=x^{2}+\frac{a^{2}}{3}.
Рассмотрим сечение тетраэдра плоскостью, проходящей через параллельные прямые EE_{1}
и OQ
. Если P
— ортогональная проекция точки E
на прямую OQ
, то
R^{2}=OE^{2}=OP^{2}+PE^{2}=|OQ-OP|^{2}+QE^{2}=|OQ-EE_{1}|^{2}+(QF+FE)^{2}=
=\left(OQ-\frac{1}{3}DF\right)^{2}+\left(FC+\frac{2}{3}FC\right)^{2}=\left(x-\frac{1}{3}a\sqrt{\frac{2}{3}}\right)^{2}+\left(\frac{5}{3}\cdot\frac{a}{\sqrt{3}}\right)^{2}=
=\left(x-\frac{a\sqrt{2}}{3\sqrt{3}}\right)^{2}+\left(\frac{5a}{3\sqrt{3}}\right)^{2}=x^{2}-\frac{2ax\sqrt{2}}{3\sqrt{3}}+\frac{2a^{2}}{27}+\frac{25a^{2}}{27}=x^{2}-\frac{2ax\sqrt{2}}{3\sqrt{3}}+a^{2}.
Из уравнения x^{2}+\frac{a^{2}}{3}=x^{2}-\frac{2ax\sqrt{2}}{3\sqrt{3}}+a^{2}
находим, что x=\frac{a\sqrt{3}}{\sqrt{2}}
. Следовательно,
R^{2}=x^{2}+\frac{a^{2}}{3}=\frac{3}{2}a^{2}+\frac{a^{2}}{3}=\frac{11}{6}a^{2},~R=a\sqrt{\frac{11}{6}}.
Источник: Вступительный экзамен в МФТИ. — 1999, билет 1, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 99-1-6, с. 381

