8929. Сторона основания ABCD
правильной пирамиды SABCD
равна 2, высота пирамиды, опущенная на основание, равна 2\sqrt{2}
. На рёбрах SA
и SD
расположены точки E
и F
так, что AE=2ES
, SF=5DF
. Через точки E
и F
проведена плоскость \alpha
, параллельная CD
. Найдите:
1) площадь фигуры, полученной при пересечении пирамиды плоскостью \alpha
;
2) радиус сферы с центром в точке A
, касающейся плоскости \alpha
;
3) угол между плоскостью \alpha
и плоскостью ABC
.
Ответ. 1) \frac{77}{36}
; 2) \frac{40\sqrt{2}}{33}
; 3) \arccos\frac{7}{11}
.
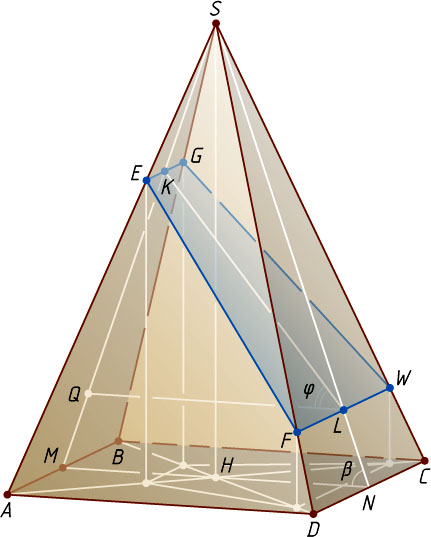
Решение. Пусть M
и N
— середины сторон соответственно AB
и CD
квадрата ABCD
(рис. 1), H
— центр квадрата. Тогда SNH
— линейный угол двугранного угла между боковой гранью и основанием пирамиды SABCD
. Обозначим \angle SNH=\beta
. Из прямоугольного треугольника SNH
находим, что
SN=\sqrt{SH^{2}+NH^{2}}=\sqrt{8+1}=3,~\sin\beta=\frac{SH}{SN}=\frac{2\sqrt{2}}{3}.
Плоскость \alpha
параллельна прямой CD
, а значит, и прямой AB
. Плоскость SCD
проходит через прямую CD
, параллельную плоскости \alpha
, и пересекает эту плоскость, поэтому прямая пересечения плоскостей \alpha
и SCD
параллельна CD
. Аналогично, прямая пересечения плоскостей \alpha
и SAB
параллельна прямой AB
, а значит, и прямой CD
. Пусть плоскость \alpha
пересекает боковые рёбра SB
и SC
пирамиды в точках G
и W
соответственно. Тогда
EG\parallel AB,~FW\parallel CD,~EG=\frac{1}{3}AB=\frac{2}{3},~FW=\frac{5}{6}CD=\frac{5}{3}.
Сечение пирамиды плоскостью \alpha
— равнобедренная трапеция FEGW
с основаниями EG=\frac{2}{3}
и FW=\frac{5}{3}
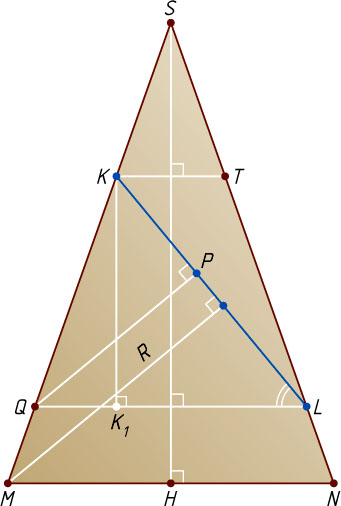
. Рассмотрим сечение пирамиды плоскостью MSN
. В этой плоскости лежат середины K
и L
оснований соответственно EG
и FW
трапеции FEGW
, а также центр H
квадрата ABCD
, при этом KL
— высота трапеции EFGW
. Пусть прямая, проходящая через точку L
параллельно MN
пересекает отрезок SM
в точке Q
, а прямая, проходящая через точку K
параллельно MN
пересекает отрезок SN
в точке T
. Тогда
TL=KQ=SQ-SK=\frac{5}{6}SM-\frac{1}{3}MN=\frac{1}{2}MN=\frac{3}{2},
KT=\frac{1}{3}MN=\frac{2}{3},~QL=\frac{5}{6}MN=\frac{5}{3}.
Пусть K_{1}
— проекция точки K
на QL
. Тогда
KK_{1}=KQ\sin\angle KQL=KQ\sin\angle SMH=\frac{3}{2}\cdot\sin\beta=\frac{3}{2}\cdot\frac{2\sqrt{2}}{3}=\sqrt{2}.
Из равнобедренной трапеции KQLT
находим, что
K_{1}L=\frac{1}{2}(KT+LQ)=\frac{1}{2}\left(\frac{2}{3}+\frac{5}{3}\right)=\frac{7}{6},
KL=\sqrt{KK_{1}^{2}+K_{1}L^{2}}=\sqrt{2+\frac{49}{36}}=\frac{11}{6}.
Следовательно,
S_{FEGW}=\frac{1}{2}(EG+FW)\cdot KL=\frac{1}{2}\left(\frac{2}{3}+\frac{5}{3}\right)\cdot\frac{11}{6}=\frac{77}{36}
Заметим, что угол между плоскостями \alpha
и ABCD
равен углу между плоскостью \alpha
и плоскостью, проходящей через прямую FW
параллельно плоскости ABCD
, а линейный угол этого двугранного угла — это угол KLQ
. Обозначим \angle KLQ=\varphi
. Из прямоугольного треугольника KLK_{1}
находим, что
\cos\varphi=\frac{K_{1}L}{KL}=\frac{\frac{7}{6}}{\frac{11}{6}}=\frac{7}{11}.
Пусть R
— радиус сферы с центром в точке A
, касающейся плоскости \alpha
, P
— основание перпендикуляра, опущенного из точки Q
на KL
(рис. 2). Тогда R
— расстояние от точки A
до плоскости \alpha
, а так как прямая AB
параллельна этой плоскости, то расстояние от точки M
до плоскости \alpha
также равно R
. Из соотношения \frac{KQ}{KM}=\frac{\frac{3}{2}}{\frac{2}{3}\cdot3}=\frac{3}{4}
следует, что R=\frac{4}{3}QP
.
Записав двумя способами площадь треугольника KLQ
, получим равенство KL\cdot QP=QL\cdot KK_{1}
, откуда
QP=\frac{QL\cdot KK_{1}}{KL}=\frac{\frac{5}{3}\sqrt{2}}{\frac{11}{6}}=\frac{10\sqrt{2}}{11}.
Следовательно,
R=\frac{4}{3}QP=\frac{4}{3}\cdot\frac{10\sqrt{2}}{11}=\frac{40\sqrt{2}}{33}.
Источник: Вступительный экзамен в МФТИ. — 1999, билет 5, № 6
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 99-5-6, с. 384

