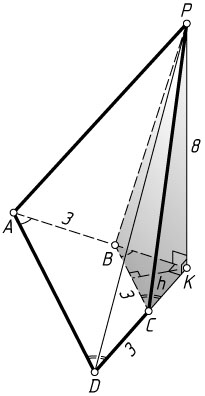
9568. Основание пирамиды PABCD
— трапеция ABCD
, причём \angle BAD+\angle ADC=90^{\circ}
. Плоскости PAB
и PCD
перпендикулярны плоскости основания, прямые AB
и CD
пересекаются в точке K
.
а) Докажите, что плоскости PAB
и PCD
перпендикулярны.
б) Найдите объём пирамиды PKBC
, если AB=BC=CD=3
, а высота пирамиды равна 8.
Ответ. 6.
Решение. а) Плоскости PAB
и PCD
, перпендикулярные плоскости ABC
, пересекаются по прямой, проходящей через точку P
перпендикулярно плоскости ABC
(см. задачу 9104). Значит, PK
— высота данной пирамиды.
Прямые AK
и DK
перпендикулярны, так как
\angle AKD=180^{\circ}-(\angle BAD+\angle ADC)=180^{\circ}-90^{\circ}=90^{\circ},
а так как AKD
— линейный угол двугранного угла, образованного плоскостями PAB
и PCD
, то эти плоскости перпендикулярны.
б) Треугольник BKC
равнобедренный и прямоугольный, так как \angle KBC=\angle KCB=45^{\circ}
. Его высота, опущенная на гипотенузу BC
половине гипотенузы, т. е. h=\frac{1}{2}BC=\frac{3}{2}
. Тогда
S_{\triangle BKC}=\frac{1}{2}BC\cdot h=\frac{1}{2}\cdot3\cdot\frac{3}{2}=\frac{9}{4}.
Следовательно, объём пирамиды PKBC
равен
\frac{1}{3}S_{\triangle BKC}\cdot PK=\frac{1}{3}\cdot\frac{9}{4}\cdot8=6.
