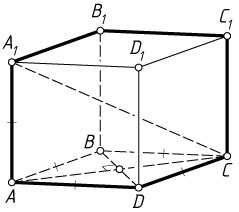
9590. Основанием прямой четырёхугольной призмы ABCDA_{1}B_{1}C_{1}D_{1}
является ромб ABCD
, AB=AA_{1}
.
а) Докажите, что прямые A_{1}C
и BD
перпендикулярны.
б) Найдите объём призмы, если A_{1}C=BD=2
.
Ответ. \frac{4\sqrt{6}}{5}
.
Решение. а) Диагонали ромба перпендикулярны, поэтому AC\perp BD
. Данная призма прямая, поэтому AA_{1}
— перпендикуляр к плоскости ABC
. Значит, прямая AC
— ортогональная проекция наклонной A_{1}C
на эту плоскость. Следовательно, по теореме о трёх перпендикулярах AC_{1}\perp BD
.
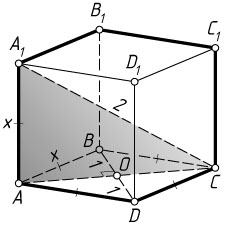
б) Обозначим AB=AA_{1}=x
. Пусть O
— центр ромба ABCD
. Из прямоугольного треугольника AOB
находим, что
AO^{2}=AB^{2}-BO^{2}=x^{2}-1,
Значит, AC=2AO=2\sqrt{x^{2}-1}
.
Из прямоугольного треугольника CAA_{1}
получаем, что
A_{1}C^{2}=AA_{1}^{2}+AC^{2},~\mbox{или}~4=x^{2}+4(x^{2}-1),
откуда x=\sqrt{\frac{8}{5}}=\frac{2\sqrt{2}}{\sqrt{5}}
. Следовательно,
V_{ABCDA_{1}B_{1}C_{1}D_{1}}=S_{ABCD}\cdot AA_{1}=\frac{1}{2}AC\cdot BD\cdot AA_{1}=
=\frac{1}{2}\cdot2\sqrt{x^{2}-1}\cdot2\cdot x=\frac{1}{2}\cdot2\sqrt{\frac{8}{5}-1}\cdot2\cdot\frac{2\sqrt{2}}{\sqrt{5}}=\frac{4\sqrt{6}}{5}.
Источник: ЕГЭ. — 2017

