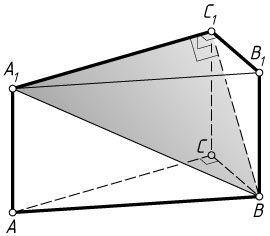
9594. Основанием прямой треугольной призмы ABCA_{1}B_{1}C_{1}
является прямоугольный треугольник ABC
с прямым углом C
. Диагонали боковых граней AA_{1}B_{1}B
и BB_{1}C_{1}C
равны 15 и 9 соответственно, AB=13
.
а) Докажите, что треугольник BA_{1}C_{1}
прямоугольный.
б) Найдите объём пирамиды AA_{1}C_{1}B
.
Ответ. 20\sqrt{14}
.
Решение. а) Прямая A_{1}C_{1}
перпендикулярна двум пересекающимся прямым B_{1}C_{1}
(треугольник A_{1}B_{1}C_{1}
прямоугольный с прямым углом C_{1}
) и CC_{1}
(так как призма прямая). Значит, A_{1}C_{1}
— перпендикуляр к этой плоскости. Следовательно, A_{1}C_{1}\perp BC_{1}
, т. е. треугольник BA_{1}C_{1}
прямоугольный с прямым углом C_{1}
.
б) Из прямоугольных треугольников A_{1}BC_{1}
, A_{1}B_{1}C_{1}
и BB_{1}C_{1}
находим, что
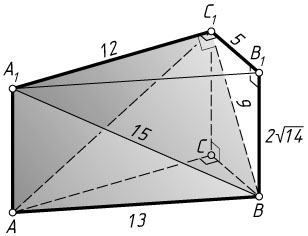
A_{1}C_{1}=\sqrt{A_{1}B^{2}-BC_{1}^{2}}=\sqrt{15^{2}-9^{2}}=12,
B_{1}C_{1}=\sqrt{A_{1}B_{1}^{2}-A_{1}C_{1}^{2}}=\sqrt{13^{2}-12^{2}}=5,
BB_{1}=\sqrt{BC_{1}^{2}-B_{1}C_{1}^{2}}=\sqrt{9^{2}-5^{2}}=2\sqrt{14}.
Прямая BC
перпендикулярна двум пересекающимся прямым AC
и CC_{1}
плоскости AA_{1}C_{1}
, поэтому BC
— высота пирамиды AA_{1}C_{1}B
. Следовательно,
V_{AA_{1}C_{1}B}=\frac{1}{3}S_{\triangle AA_{1}C_{1}}\cdot BC=\frac{1}{3}\cdot\frac{1}{2}A_{1}C_{1}\cdot AA_{1}\cdot BC=
=\frac{1}{6}A_{1}C_{1}\cdot BB_{1}\cdot BC=\frac{1}{6}\cdot12\cdot2\sqrt{14}\cdot5=20\sqrt{14}.
Источник: ЕГЭ. — 2017

